book: 수식이 보이는 공학수학 (Engineering Mathematics)

chapter 08 행렬과 행렬식 (Matrices and Determinant)

알아 두어야 할 개념과 공식

1. 벡터, 스칼라

길이, 무게 등 크기만으로 정해지는 물리량을 스칼라(scalar)라고 한다. 이에 반해 힘, 속도 등과 같이 크기와 동시에 방향까지 생각해야 하는 물리량을 벡터(vector)라고 한다. 벡터는 흔히 화살표를 사용해 $\vec{A}$와 같이 표현하거나 문자를 굵게 하여 A와 같이 표현한다.

2. 행렬의 상등

다음 식이 성립하는 경우에 행렬 A와 행렬 B가 같다고 한다.

\[A=\begin{bmatrix} a_{11} & a_{12} \\\ \ a_{21} & a_{22} \end{bmatrix}, \ B=\begin{bmatrix} b_{11} & b_{12} \\\ \ b_{21} & b_{22} \end{bmatrix}\]

일 때,

\[A=B \Leftrightarrow \ \begin{bmatrix}\ a_{11} & a_{12} \\\ \ a_{21} & a_{22} \end{bmatrix} \Leftrightarrow \ \begin{bmatrix}\ a_{11} & a_{12} \\\ \ a_{21} & a_{22} \end{bmatrix} \Leftrightarrow \ a_{11}=b_{11}, a_{12}=b_{12}, a_{21}=b_{21}, a_{22}=b_{22}\]

3. 정방행렬, 단위행렬, 스칼라행렬, 대각행렬, 삼각행렬

같은 수의 행과 열을 가진 행렬을 정방행렬^{square matrix} 이라고 한다. 정방행렬에서 주대각 원소들은 1 값을 갖고, 나머지 원소들은 0값을 갖는 행렬을 단위행렬^{unit matrix} 이라고 하고, 보통 I 로 나타낸다. 또한 주대각 원소들이 같은 값으로 이루어져 있으면 스칼라 행렬^{scalar matrix} 이라고 한다. 주대각 원소만 0이 아닌 행렬을 대각행렬^{diagnal matrix} 이라고 하며, 주대각선 아래쪽의 모든 원소들이 0인 경우를 위삼각행렬^{upper triangular matrix} , 위쪽의 모든 원소들이 0인 경우를 아래삼각행렬^{lower triangular matrix} 이라고 한다.

• 정방행렬 \(A=\begin{bmatrix}\ a_{11} & a_{12} & \cdots & a_{1n} \\\ \ a_{21} & a_{22} & \cdots & a_{2n} \\\ \ \vdots & \vdots & \ddots & \vdots \\\ \ a_{n1} & a_{n2} & \cdots & a_{nn} \end{bmatrix}\)
• 단위행렬 \(I=\begin{bmatrix}\ 1 & 0 & \cdots & 0 \\\ \ 0 & 1 & \cdots & 0 \\\ \ \vdots & \vdots & \ddots & \vdots \\\ \ 0 & 0 & \cdots & 1 \end{bmatrix}\)
• 스칼라행렬 \(S=\begin{bmatrix}\ a & 0 & \cdots & 0 \\\ \ 0 & a & \cdots & 0 \\\ \ \vdots & \vdots & \ddots & \vdots \\\ \ 0 & 0 & \cdots & a \end{bmatrix}\)
• 대각행렬 \(D=\begin{bmatrix}\ a_1 & 0 & \cdots & 0 \\\ \ 0 & a_2 & \cdots & 0 \\\ \ \vdots & \vdots & \ddots & \vdots \\\ \ 0 & 0 & \cdots & a_n \end{bmatrix}\)
• 위삼각행렬 \(U=\begin{bmatrix}\ a_{11} & a_{12} & a_{13} \\\ \ 0 & a_{22} & a_{23} \\\ \ 0 & 0 & a_{33} \end{bmatrix}\)
• 아래삼각행렬 \(L=\begin{bmatrix}\ a_{11} & 0 & 0 \\\ \ a_{21} & a_{22} & 0 \\\ \ a_{31} & a_{32} & a_{33} \end{bmatrix}\)

8.1 행렬의 기본 개념

8.1.1 행렬이란?

행렬^matrix 이란 다음에 나타낸 식처럼 수나 함수들을 괄호 안에 행과 열로 배열해놓은 것을 말한다.

• 식(8.1) \(\begin{bmatrix}\ 1 & 2 & 3 \\\ \ 6 & 5 & 6 \end{bmatrix}, \begin{bmatrix}\ a & b \\\ \ c & d \end{bmatrix}, \begin{bmatrix}\ 3 \\\ \ 1 \end{bmatrix}, \begin{bmatrix}\ f(x) & g(x) & h(x) \end{bmatrix}\) 식(8.1)에서 괄호 안에 배열되어 있는 수나 함수들을 그 행렬의 원소^element 라고 하며, 이와 같은 형태의 행렬을 일반적으로 다음과 같이 표기한다.
• 식(8.2) \(\begin{bmatrix}\ a_{11} & a_{12} & \cdots & a_{1n} \\\ \ a_{21} & a_{22} & \cdots & a_{2n} \\\ \ \vdots & \vdots & \ddots & \vdots \\\ \ a_{m1} & a_{m2} & \cdots & a_{mn} \end{bmatrix}\) 식(8.2)의 경우, 원소 $a_{11}$ 에서 $a_{1n}$ 까지 가로로 나열되어 있는 배열을 행^row 이라고 하고, 원소 $a_{11}$ 에서 $a_{m1}$ 까지 세로로 나열되어 있는 배열을 열^column 이라고 한다. 식(8.2)는 m개의 행과 n개의 열로 이루어져 있는 행렬인데, 이와 같은 경우 mxn이라고 쓰고, ‘m by n’이라고 읽는다. 하나의 행이나 하나의 열로 표현되는 행렬을 벡터라고 부르기도 한다. 즉,
• 식(8.3) \(\begin{bmatrix}\ a_1 & a_2 & \cdots & a_n \end{bmatrix}\) 과 같이 하나의 행으로 표현되어 있는 행렬을 행벡터^{row vector} 라고 하고
• 식(8.4) \(\begin{bmatrix}\ b_1 \\\ \ b_2 \\\ \ \vdots \\\ \ b_n \end{bmatrix}\) 과 같이 하나의 열로 표현되어 있는 행렬을 열벡터^{column vector} 라고 한다.

식(8.2)는 다음과 같이 나타낼 수도 있다.

• 식(8.5) \(A= \begin{bmatrix}\ a_{jk} \end{bmatrix} = \begin{bmatrix}\ a_{11} & a_{12} & \cdots & a_{1n} \\\ \ a_{21} & a_{22} & \cdots & a_{2n} \\\ \ \vdots & \vdots & \ddots & \vdots \\\ \ a_{m1} & a_{m2} & \cdots & a_{mn} \end{bmatrix}\)

$\begin{bmatrix} a_{jk} \\ \end{bmatrix}$ 에서 사용한 아래첨자인 j와 k는 각각 행과 열을 나타낸다.

임의의 행렬에서의 대각선을 주대각선^{principal diagonal} 이라고 한다. 주대각선에 있는 원소 $a_{11}, a_{12}, \cdots, a_{nn}$ 을 대각 원소라 한다.

8.1.2 행렬의 기본 연산

지금부터 행렬의 합과 차를 구하는 연산과 행렬에 스칼라 값을 곱하는 연ㅅ나에 대해 살펴보자. 이를 위해 먼저 행렬의 상등에 대해 살펴볼 필요가 있다.

행렬의 상등

행렬의 상등이란 두 행렬이 같다는 의미다. 다음과 같은 행렬 A와 행렬 B가 존재할 경우,

• 식(8.6) \(A=\begin{bmatrix} a_{jk} \end{bmatrix}=m \times n \text{행렬}, B= \begin{bmatrix} b_{jk} \end{bmatrix}=p \times q \text{행렬}\) \(m=p, n=q, \begin{bmatrix} a_{jk} \end{bmatrix}=\begin{bmatrix} b_{jk} \end{bmatrix} \text(모든 j, k에 대해)\) 식(8.6)을 만족할 때, 두 행렬 A와 B는 상등^equl이라 하고, A=B로 나타낸다. 이 때 m=p, n=q이므로 두 행렬은 같은 크기^size를 갖는다고 한다. 따라서 크기가 같아야만 행렬이 상등할 수 있다.

행렬 간의 합과 차

행렬의 상등과 마찬가지로 행렬 간의 합과 차도 행렬의 크기가 같을 때에만 계산할 수 있다. 즉 크기가 2×3으로 똑같은 행렬 \(A=\begin{bmatrix}\ a_{11} & a_{12} & a_{13} \\\ \ a_{21} & a_{22} & a_{23} \end{bmatrix}, B=\begin{bmatrix}\ b_{11} & b_{12} & b_{13} \\\ \ b_{21} & b_{22} & b_{23} \end{bmatrix}\) 가 있을 때, 두 행렬의 합 A+B와 차 A-B는 \(A+B=\begin{bmatrix}\ a_{11} & a_{12} & a_{13} \\\ \ a_{21} & a_{22} & a_{23} \end{bmatrix}+ \begin{bmatrix}\ b_{11} & b_{12} & b_{13} \\\ \ b_{21} & b_{22} & b_{23} \end{bmatrix}= \begin{bmatrix}\ a_{11}+b_{11} & a_{12}+b_{12} & a_{13}+b_{13} \\\ \ a_{21}+b_{21} & a_{22}+b_{22} & a_{23}+b_{23} \end{bmatrix}\) \(A-B=\begin{bmatrix}\ a_{11} & a_{12} & a_{13} \\\ \ a_{21} & a_{22} & a_{23} \end{bmatrix}- \begin{bmatrix}\ b_{11} & b_{12} & b_{13} \\\ \ b_{21} & b_{22} & b_{23} \end{bmatrix}= \begin{bmatrix}\ a_{11}-b_{11} & a_{12}-b_{12} & a_{13}-b_{13} \\\ \ a_{21}-b_{21} & a_{22}-b_{22} & a_{23}-b_{23} \end{bmatrix}\) 와 같이 정의할 수 있다.

행렬과 스칼라의 곱

행렬에 스칼라(상수)를 곱하는 것은 다음과 같이 정의할 수 있다. 크기가 m×n인 행렬 A와 스칼라 c의 곱은 cA로 나타내며, 행렬 A의 각 원소에 스칼라 c를 곱한 것이 cA의 원소가 된다. 행렬과 스칼라의 곱을 식으로 나타내면 다음과 같다.

• 식(8.7) \(cA=c \begin{bmatrix} a_{jk} \end{bmatrix}=\begin{bmatrix} ca_{jk} \end{bmatrix}\)

즉, 다음과 같이 계산된다.

\[cA=c \begin{bmatrix}\ a_{11} & a_{12} & a_{13} \\\ \ a_{21} & a_{22} & a_{23} \end{bmatrix}= \begin{bmatrix}\ ca_{11} & ca_{12} & ca_{13} \\\ \ ca_{21} & ca_{22} & ca_{23} \end{bmatrix}\]

8.1.3 행렬의 전치

행렬의 전치^{transposition} 란 임의의 행렬의 열과 행을 바꿔 새로운 행렬을 구성한다는 의미다. 즉 m×n 행렬 $A=\begin{bmatrix} a_{jk} \end{bmatrix}$를 \(A=\begin{bmatrix} a_{jk} \end{bmatrix}= \begin{bmatrix}\ a_{11} & a_{12} & \cdots & a_{1n} \\\ \ a_{21} & a_{22} & \cdots & a_{2n} \\\ \ \vdots & \vdots & \ddots & \vdots \\\ \ a_{m1} & a_{m2} & \cdots & a_{mn} \end{bmatrix}\) 과 같이 나타낼 때, 열과 행을 서로 바꾼 새로운 행렬

• 식(8.8) \(A^T=\begin{bmatrix} a_{kj} \end{bmatrix}= \begin{bmatrix}\ a_{11} & a_{21} & \cdots & a_{m1} \\\ \ a_{12} & a_{22} & \cdots & a_{m2} \\\ \ \vdots & \vdots & \ddots & \vdots \\\ \ a_{1n} & a_{2n} & \cdots & a_{mn} \end{bmatrix}\)

을 행렬 $A=\begin{bmatrix} a_{jk} \end{bmatrix}$의 전치행렬^{transposed matrix} 이라 하고, $A^T=\begin{bmatrix} a_{kj} \end{bmatrix}$ 로 나타낸다.

행렬이 전치되는 과정에서 행과 열을 표시하는 아래첨자 jk가 kj로 바뀐 것을 보면 행과 열이 바뀌었음을 확인할 수 있따. 즉 행렬 A에서 ‘j행 k열’이었던 원소가 전치행렬 A^T에서는 ‘k행 j열’에 있는 원소가 되는 것이다.

대칭행렬과 반대칭행렬

전치행렬과 함께 생각할 수밖에 없는 행렬로 대칭행렬과 반대칭행렬이 있다. 먼저 다음 식과 같이

• 식(8.9) \(A^T(a_{kj})=A(a_{jk})\)

를 만족하는 정방행렬을 대칭행렬^{symmetric matrix} 이라고 한다. 한편, 다음과 같은 식

• 식(8.10) \(A^T(a_{kj})=-A(-a_{jk})\)

와 같이 전치행렬이 원래 행렬의 음^negative이 되는 정방행렬을 반대칭행렬^{skew-symmetric matrix} 이라고 한다. 식(8.10)의 괄호 안의 내용을 비교하면 a_kj=-a_jk가 되므로 k=j인 경우에 a_jj=-a_jj가 성립한다. 결과적으로 2a_jj=0, 즉 a_jj=0이 되기 때문에 반대칭행렬은 주대각선에 위치하는 원소들이 모두 0이 되는 성질을 갖는다.

8.2 행렬의 곱

8.2.1 두 행렬 간의 곱

m×n 행렬 $A=\begin{bmatrix} a_{jk} \end{bmatrix}$와 p×q 행렬 $B=\begin{bmatrix} b_{jk} \end{bmatrix}$ 의 곱이 되는 행렬 C=AB가 정의되기 위해서는 n=p가 되어야 한다. 각각의 행렬 측에서 보면, 첫번째 행렬인 A의 열의 숫자와 두번째 행렬인 B의 행의 숫자가 같아야 한다는 것이다. 그런 조건이 성립할 때, 두 행렬의 곱인 C가 정의될 수 있고, 그 때 행렬 C의 크기는 행렬 A의 크기인 m×n과 행렬 B의 크기인 p×q(=n×q)가 곱해진 크기인 m×q가 된다.

• 식(8.11) \(c_{jk}=\sum_{l=1}^{n} {a_{jl} b_{lk}} = a_{j1}b_{1k}+a_{j2}b_{2k}+\cdots+a_{jn}b_{nk}\) \((j=1,2,\cdots,m \textrm{ 그리고 } k=1,2,\cdots,q)\)

벡터의 내적

벡터 a와 b의 내적^{inner product} 은 다음과 같이 정의된다.

• 식(8.13) \(a \cdot b = a_1 b_1 + a_2 b_2 + \cdots + a_n b_n = \sum_{l=1}^{n} {a_l b_l}\)

식(8.13)과 같은 벡터의 내적을 행렬의 관점으로 보면, 다음과 같이 행벡터 a와 열벡터 b의 곱으로 볼 수 있다.

• 식(8.14) \(a \cdot b = \begin{bmatrix}a_1 & \cdots & a_n \end{bmatrix} \cdot \begin{bmatrix}b_1 \\\ \vdots \\\ b_n \end{bmatrix} = a_1 b_1 + a_2 b_2 + \cdots + a_n b_n = \sum_{l=1}^{n} {a_l b_l}\)

행렬의 곱의 성질

행렬의 곱이 수와 유사한 성질을 갖는 경우

행렬의 곱이 수와 비슷한 성질을 갖는 경우는 다음과 같은 식으로 나타낼 수 있다.

• 식(8.15) \(cAB=c(AB)=(cA)B=A(cB)\)
• 식(8.16) \(ABC=A(BC)=(AB)C\)
• 식(8.17) \((A+B)C=AC+BC\)
• 식(8.18) \(C(A+B)=CA+CB\)

행렬의 곱이 수와 다른 성질을 갖는 경우

행렬의 곱이 수와 다른 성질을 갖는 경우는 다음과 같다.

• 일반적으로 $AB \neq BA$ 다. 이러한 성질에 대해 행렬의 곱은 비가환적(not commutative)이라고 한다. 즉 행렬의 곱은 교환법칙이 성립하지 않는다.
• $AB=0$ 이 반드시 $A=0, B=0$ 이나 $BA=0$ 을 의미하는 것은 아니다.
• $AC=AD$ 가 반드시 $C=D$ 를 의미하는 것은 아니다. ( $A \neq B$ 인 경우 포함)

행렬의 곱의 전치

행렬의 곱이 전치되는 경우는 다음과 같이 각 행렬의 전치행렬을 구하여 순서를 바꿔서 곱한 것과 같은 결과를 얻는다.

• 식(8.20) \((AB)^T=B^T A^T\)

8.3 행렬과 선형 연립방정식

8.3.1 선형 연립방정식

n개의 변수 $x_1, x_2, \cdots, x_n$를 갖는 m개의 방정식으로 이루어진 선형 연립방정식^{linear system}은 다음과 같이 나타낼 수 있다.

• 식(8.21) \(\begin{cases} a_{11} x_1 + a_{12} x_2 + \cdots + a_{1n} x_n = r_1\\\ \ a_{21} x_1 + a_{22} x_2 + \cdots + a_{2n} x_n = r_2\\\ \ \vdots\\\ \ a_{m1} x_1 + a_{m2} x_2 + \cdots + a_{mn} x_n = r_m \end{cases}\)

여기서 $a_{11}, a_{12}, \cdots, a_{mn}$ 은 주어진 상수로, 선형 연립방정식의 계수다. $r_1, \cdots, r_m$ 역시 주어진 상수이며, $r_1, \cdots, r_m$ 모두가 0이면 제차 연립방정식^{homogeneous linear system} 이라고 하고, 그 중 하나라도 0이 아니면 비체차 연립방정식^{non-homogeneous linear system} 이라고 한다. 선형 연립방정식의 변수인 $x_1, x_2, \cdots, x_n$ 이 m개의 방정식을 모두 만족할 수 있는 수의 집합으로 얻어질 때, 그 수의 집합을 선형 연립방정식의 해^solution 이라고 한다. 또 선형 연립방정식의 해가 되는 수의 집합을 원소로 하여 이루어진 벡터를 해벡터^{solution vector} 라고 한다. 그러면 행렬의 곱과 행렬의 상등을 이용하여 식(8.21)의 선형 연립방정식을 다음과 같은 행렬로 표현할 수 있다.

• 식(8.22) \(\begin{bmatrix}\ a_{11} & a_{12} & \cdots & a_{1n} \\\ \ a_{21} & a_{22} & \cdots & a_{2n} \\\ \ \vdots & \vdots & \ddots & \vdots \\\ \ a_{m1} & a_{m2} & \cdots & a_{mn} \end{bmatrix} \cdot \begin{bmatrix}\ x_1 \\\ \ x_2 \\\ \ \vdots \\\ \ x_n \end{bmatrix}= \begin{bmatrix}\ r_1 \\\ \ r_2 \\\ \ \vdots \\\ \ r_m \end{bmatrix}\)

식(8.22)의 각각의 행렬을 다음과 같이 둘 수 있다. \(A=\begin{bmatrix}\ a_{11} & a_{12} & \cdots & a_{1n} \\\ \ a_{21} & a_{22} & \cdots & a_{2n} \\\ \ \vdots & \vdots & \ddots & \vdots \\\ \ a_{m1} & a_{m2} & \cdots & a_{mn} \end{bmatrix}, x=\begin{bmatrix}\ x_1 \\\ \ x_2 \\\ \ \vdots \\\ \ x_n \end{bmatrix}, r=\begin{bmatrix}\ r_1 \\\ \ r_2 \\\ \ \vdots \\\ \ r_m \end{bmatrix}\)

이때 A를 계수행렬 이라고 하는데, 계수행렬은 영행렬이 되어서는 안되며, x는 n개, r은 m개의 원소를 가진 행렬이라는 점에 유의해야 한다. 또 계수행렬 A의 마지막 열에 열행렬 r의 원소를 추가하여 이루어진 \(\widetilde{A}=\begin{bmatrix}\ a_{11} & a_{12} & \cdots & a_{1n} & r_1\\\ \ a_{21} & a_{22} & \cdots & a_{2n} & r_2\\\ \ \vdots & \vdots & \ddots & \vdots & \vdots\\\ \ a_{m1} & a_{m2} & \cdots & a_{mn} & r_m \end{bmatrix}\)

와 같은 형태의 행렬을 첨가행렬^{augmented matrix} 이라고 한다. 첨가행렬은 선형 연립방정식이 가진 모든 수를 포함한 행렬을 말한다.

8.3.2 가우스 소거법

가우스 소거법^{Gauss elimination} 은 선형 연립방정식으로부터 첨가행렬을 추출하여 소거과정을 되풀이하면서 해를 구하는 방법이다. 여기에서는 한가지 예로 가우스 소거법을 사용하여 선형 연립방정식의 해를 구하는 과정을 살펴볼 것이다.

그러면 다음과 같은 선형 연립방정식과 그로부터 얻어진 첨가행렬을 나열한 후 가우스 소거법에 대해 논의하기로 하자.

\[\begin{cases} x_1 - x_2 - 2 x_3 = 3\\\ \ 2 x_1 - x_2 + x_3 = 5\\\ \ -3 x_1 + 2 x_2 -5 x_3 = 4 \end{cases}\] \[\begin{bmatrix}\ 1 & -1 & -2 & 3 \\\ \ 2 & -1 & 1 & 5 \\\ \ -3 & 2 & -5 & 4 \end{bmatrix}\]

위의 연립방정식에서 첫번째 방정식을 추축방정식^{pivot equation} 이라고 하고, 이때 x₁의 계수를 추축^pivot 이라고 한다.

\[\begin{align} x_1 - x_2 - 2 x_3 = 3\\\ \ 2 x_1 - x_2 + x_3 = 5\\\ \ -3 x_1 + 2 x_2 -5 x_3 = 4 \end{align}\] \[\begin{bmatrix}\ \color{red}{1} & -1 & -2 & 3 \\\ \ \color{blue}{2} & -1 & 1 & 5 \\\ \ \color{blue}{-3} & 2 & -5 & 4 \end{bmatrix}\]

위의 첨가행렬에 빨간색 원소가 추축에 해당되는 수이다. 즉, $x_1$ 의 계수가 1이란 의미다. 이때 먼저 해야할 일은 추축의 아래에 파란색 원소들인 나머지 방정식의 $x_1$ 항을 소거하는 것이다. 그렇게 하기 위해 다음과 같은 연산을 행하면

\[(2)-2(1)\\\ \ \rightarrow (2 x_1 - x_2 + x_3)-2(x_1 - x_2 - 2 x_3) = 5 - 2 \times 3 \\\ \ \rightarrow x_2 + 5 x_3 = -1\] \[(3)+3(1)\\\ \ \rightarrow (-3 x_1 + 2 x_2 -5 x_3) + 3(x_1 - x_2 - 2 x_3) = 4 + 3 \times 3 \\\ \ \rightarrow -x_2 - 11 x_3 = 13\]

과 같이 되고, $(2)-2(1)$ 와 $(3)+3(1)$ 로 계산한 식은 새로운 (2)와 (1)이 된다. 이와 같은 결과를 연립방정식과 첨가행렬에 반영하면 다음과 같이 된다.

\[\begin{align} x_1 - x_2 - 2 x_3 = 3\\\ \ x_2 + 5 x_3 = -1\\\ \ -x_2 - 11 x_3 = 13 \end{align}\] \[\begin{bmatrix}\ 1 & -1 & -2 & 3 \\\ \ 0 & \color{red}{1} & 5 & -1 \\\ \ 0 & \color{blue}{-1} & -11 & 13 \end{bmatrix}\]

위 식에서 새로운 추축은 첨가행렬에서 빨간색 원소인 1, 즉 $x_2$ 의 계수가 되고, 이를 기준으로 다음 식의 $x_2$ 를 소거하려면

\[(6)+(5) \\\ \ \rightarrow (-x_2 - 11 x_3) + (x_2 + 5 x_3) = 13-1 \\\ \ \rightarrow -6 x_2 = 12\]

와 같이 계산해야 하고, 이를 반영하면 다음과 같은 결과를 얻는다.

\[\begin{align} x_1 - x_2 - 2 x_3 = 3\\\ \ x_2 + 5 x_3 = -1\\\ \ -6 x_3 = 12 \end{align}\] \[\begin{bmatrix}\ 1 & -1 & -2 & 3 \\\ \ 0 & 1 & 5 & -1 \\\ \ 0 & 0 & -6 & 12 \end{bmatrix}\]

위의 연립방정식에서 (9)에서 (7)로 거슬러 올라가며 계산하면 $x_3, x_2, x_1$ 값을 순서대로 구할 수 있다. 즉, 다음과 같이 된다.

(9) $-6 x_3 = 12$ 를 풀면, $x_3 = -2$

(8) $x_2 + 5(-2)=-1$ 을 풀면, $x_2 = 9$

(7) $x_1 - 9 - 2(-2) = 3$ 을 풀면, $x_1 = 8$

이와 같이 가우스 소거법은 추축방정식과 추축을 정하고 소거를 통해 변수의 개수를 줄여가는 방법이다. 마지막으로 변수가 하나 남게 되면, 그 변수의 값을 알 수 있으므로 나머지 변수들의 값도 차례로 알 수 있다. 사실 앞에서 풀어본 연립방정식은 전통적인 방법으로 계산해도 풀 수 있을 정도로 규모가 작다. 하지만 변수가 상당히 많은 큰 규모의 방정식이라면 변수를 소거하는 체계가 잡혀있는 가우스 소거법으로 해를 구하는 것이 훨씬 간편할 것이다.

가우스 소거법에서 가능한 기본 연산에 대해 정리하면 다음과 같다.

1. 한 방정식에 0이 아닌 상수를 곱하는 것
2. 한 방정식의 상수배를 다른 방정식에 더하는 것
3. 두 방정식을 교환하는 것

위의 항목에서 3은 앞의 예에서 보지 못하 ㄴ것이다. 그러므로 가우스 소거법을 사용할 때 방정식의 순서를 교환하더라도 아무 상관이 없다는 점을 기억해 두는 것이 좋겠다. 또 첨가행렬에서 모순된 결과가 발생하면 해가 존재하지 않는 경우라는 것을 기억하자.

가우스-조던 소거법 (Gauss-Jordan elimination)

가우스-조던 소거법은 가우스 소거법을 통해 만든 좌변의 위삼각행렬을 단위행렬이 될 때까지 계속 소거를 하는 방법을 말한다.

위의 예에서,

\(\begin{bmatrix}\ 1 & -1 & -2 & 3 \\\ \ 0 & 1 & 5 & -1 \\\ \ 0 & 0 & -6 & 12 \end{bmatrix}\) 의 행렬을 가우스 소거법과 동일한 방법으로

\(\begin{bmatrix}\ 1 & 0 & 0 & 8 \\\ \ 0 & 1 & 0 & 9 \\\ \ 0 & 0 & 1 & -2 \end{bmatrix}\) 과 같이 만드는 것이다.

8.4 행렬식

8.4.1 행렬식의 정의

2차 행렬식

2×2 행렬에 대한 행렬식은 2차 행렬식^determinant 이라고 하고, 다음과 같이 정의한다. 행렬식을 나타낼 때는 앞절에서 다룬 행렬과 달리 선분을 사용한다.

• 식(8.26) \(D = \det A = \begin{vmatrix}\ a_{11} & a_{12} \\\ \ a_{21} & a_{22} \end{vmatrix} = a_{11} a_{22} - a_{12} a_{21}\)

3차 행렬식

3×3 행렬에 대한 행렬식을 3차 행렬식이라 하고, 다음과 같이 정의한다.

• 식(8.27) \(D = \begin{vmatrix}\ a_{11} & a_{12} & a_{13}\\\ \ a_{21} & a_{22} & a_{23}\\\ \ a_{31} & a_{32} & a_{33} \end{vmatrix} = a_{11} \begin{vmatrix}\ a_{22} & a_{23}\\\ \ a_{32} & a_{33} \end{vmatrix} - a_{21} \begin{vmatrix}\ a_{12} & a_{13}\\\ \ a_{32} & a_{33} \end{vmatrix} + a_{31} \begin{vmatrix}\ a_{12} & a_{13}\\\ \ a_{22} & a_{23} \end{vmatrix}\)

3차 행렬식을 기억하려면 (1) 부호가 +, -, + 순이라는 것과 (2) 각각의 2차 행렬식과 그 앞에 곱해진 원소와의 관계를 알아야 한다. 다음 행렬식을 보면 원소와 2차 행렬식의 관계에 대해 알 수 있다.

\[\begin{vmatrix}\ \color{red}{a_{11}} & a_{12} & a_{13}\\\ \ a_{21} & \color{blue}{a_{22}} & \color{blue}{a_{23}}\\\ \ a_{31} & \color{blue}{a_{32}} & \color{blue}{a_{33}} \end{vmatrix}, \begin{vmatrix}\ a_{11} & \color{blue}{a_{12}} & \color{blue}{a_{13}}\\\ \ \color{red}{a_{21}} & a_{22} & a_{23}\\\ \ a_{31} & \color{blue}{a_{32}} & \color{blue}{a_{33}} \end{vmatrix}, \begin{vmatrix}\ a_{11} & \color{blue}{a_{12}} & \color{blue}{a_{13}}\\\ \ a_{21} & \color{blue}{a_{22}} & \color{blue}{a_{23}}\\\ \ \color{red}{a_{31}} & a_{32} & a_{33} \end{vmatrix}\]

즉, 기준이 되는 원소가 $a_{11}, a_{21}, a_{31}$ 일 때, 각각의 원소에 따른 2차 행렬식은 그 원소가 속한 행과 열을 제외한 나머지 원소로 구성된다는 것이다. 이와 같이 원래의 행렬식에서 하나의 원소를 중심으로 구성되는 저차의 행렬식을 소행렬식^minor 이라고 한다.

행렬 $A=\begin{bmatrix}a_{jk}\end{bmatrix}$에 대한 소행렬식은 원소 $a_{jk}$ 를 기준으로 할 때, $A_{jk}$ 와 같이 표현한다. 즉, 식(.8.27)을 소행렬식으로 표현하면 다음과 같이 나타낼 수도 있다.

\[D = a_{11} \begin{vmatrix}\ a_{22} & a_{23}\\\ \ a_{32} & a_{33} \end{vmatrix} - a_{21} \begin{vmatrix}\ a_{12} & a_{13}\\\ \ a_{32} & a_{33} \end{vmatrix} + a_{31} \begin{vmatrix}\ a_{12} & a_{13}\\\ \ a_{22} & a_{23} \end{vmatrix} = a_{11} A_{11} - a_{21} A_{21} + a_{31} A_{31}\]

위 식에서 부호가 바뀌는 것을 포함한 여인자^cofactor 를 다음과 같이 정의할 수 있다.

• 식(8.28) \(C_{jk} = (-1)^{j+k} A_{jk}\)

여인자를 사용하면 식(8.27)을 다음과 같이 나타낼 수 있다. \(D = a_{11} \begin{vmatrix}\ a_{22} & a_{23}\\\ \ a_{32} & a_{33} \end{vmatrix} - a_{21} \begin{vmatrix}\ a_{12} & a_{13}\\\ \ a_{32} & a_{33} \end{vmatrix} + a_{31} \begin{vmatrix}\ a_{12} & a_{13}\\\ \ a_{22} & a_{23} \end{vmatrix} = a_{11} C_{11} + a_{21} C_{21} + a_{31} C_{31}\)

또한 식(8.27)의 3차 행렬식을 풀어쓰면 다음과 같이 된다.

• 식(8.29) \(\begin{vmatrix}\ a_{11} & a_{12} & a_{13}\\\ \ a_{21} & a_{22} & a_{23}\\\ \ a_{31} & a_{32} & a_{33} \end{vmatrix} = a_{11} a_{22} a_{33} - a_{11} a_{23} a_{32} + a_{21} a_{13} a_{32} - a_{21} a_{12} a_{33} + a_{31} a_{12} a_{23} - a_{31} a_{13} a_{22}\)

n차 행렬식

일반적인 경우인 n×n 정방행렬 $A = \begin{bmatrix} a_{jk} \end{bmatrix}$ 에 대한 행렬식을 n차 행렬식 이라 하고, 다음과 같이 정의한다.

• 식(8.30) \(D = \det A = \begin{vmatrix}\ a_{11} & a_{12} & \cdots & a_{1n}\\\ \ a_{21} & a_{22} & \cdots & a_{2n}\\\ \ \vdots & \vdots & \ddots & \vdots \\\ \ a_{n1} & a_{n2} & \cdots & a_{nn} \end{vmatrix}\)

$n \geq 2$ 의 경우에 대해 여인자를 활용하면, n차 행렬식은

• 식(8.31) \(D = a_{j1} C_{j1} + a_{j2} C_{j2} + \cdots + a_{jn} C_{jn}, (j=1,2,\cdots,n)\)

과 같이 첨자 j를 선택하여 행(j)에 대해 전개할 수도 있다. 또한

• 식(8.32) \(D = a_{1k} C_{1k} + a_{2k} C_{2k} + \cdots + a_{nk} C_{nk}, (n=1,2,\cdots,n)\)

와 같이 첨자 k를 선택하여 열(k)에 대해 전개할 수도 있다. 그 결과 식(8.31)과 식(8.32)는 각각 다음과 같이 나타낼 수 있다.

• 식(8.33) \(D = \sum_{k=1}^{n} a_{jk}C_{jk} = \sum_{k=1}^{n} (-1)^{j+k} a_{jk}A_{jk}, (j=1,2,\cdots,n)\)
• 식(8.34) \(D = \sum_{j=1}^{n} a_{jk}C_{jk} = \sum_{j=1}^{n} (-1)^{j+k} a_{jk}A_{jk}, (k=1,2,\cdots,n)\)

8.4.2 행렬식의 성질

행의 교환

행렬식에서 두 행을 교환하는 것은 그 행렬식의 값에 -1을 곱하는 것과 같다.

\[A = \begin{vmatrix}\ a & b \\\ \ c & d \end{vmatrix} = ad - bc,\\\ \ -B = - \begin{vmatrix}\ c & d \\\ \ a & b \end{vmatrix} \ -(cb-ad) = ad-bc\]

행의 상수배 덧셈

행렬식에서 한 행의 상수배를 다른 행에 더해도 행렬식의 값은 변하지 않는다.

\[\begin{vmatrix}\ a & b \\\ \ c & d \end{vmatrix} = ad-bc,\\\ \ \begin{vmatrix}\ a & b \\\ \ c+2a & d+2b \end{vmatrix} = a(d+2b)-(c+2a)b = ad+2ab-bc-2ab = ad-bc\]

행의 상수배

행렬식에서 한 행에 상수배를 한 것은 행렬식의 값을 상수배한 것과 같다.

\[\begin{vmatrix}\ 2a & 2b \\\ \ c & d \end{vmatrix} = 2ad-2bc,\\\ \ 2 \begin{vmatrix}\ a & b \\\ \ c & d \end{vmatrix} = 2(ad-bc) = 2ad-2bc\]

전치와 행렬식

임의의 행렬과 그 전치행렬의 행렬식 값은 동일하다.

\[A = \begin{bmatrix}\ a & b \\\ \ c & d \end{bmatrix},\\\ \det A = \begin{vmatrix}\ a & b \\\ \ c & d \end{vmatrix} = ad - bc,\\\ \ \det A^T = \begin{vmatrix}\ a & c \\\ \ b & d \end{vmatrix} = ad - bc\]

영벡터와 행렬식

행렬에 0행이나 0열(영벡터)이 존재하면, 그 행렬식의 값은 0이 된다.

\[\begin{vmatrix}\ a & b & c \\\ \ 0 & 0 & 0 \\\ \ d & e & f \end{vmatrix} = a \begin{vmatrix} \ 0 & 0 \\\ \ e & f \end{vmatrix} - 0 \begin{vmatrix}\ b & c \\\ \ e & f \end{vmatrix} + d \begin{vmatrix}\ b & c \\\ \ 0 & 0 \end{vmatrix} = a(0-0)-0(bf-ec)+d(0-0) = 0,\\\ \ \begin{vmatrix}\ g & 0 & j \\\ \ h & 0 & k \\\ \ i & 0 & l \end{vmatrix} = g \begin{vmatrix}\ 0 & k \\\ \ 0 & l \end{vmatrix} - h \begin{vmatrix}\ 0 & j \\\ \ 0 & l \end{vmatrix} + i \begin{vmatrix}\ 0 & j \\\ \ 0 & k \end{vmatrix} = g(0-0)-h(0-0)+i(0-0) = 0\]

비례하는 행(열)과 행렬식

임의의 행이나 열과 비례하는 값을 가진 행이나 열이 존재하면 그 행렬식의 값은 -이 된다. 따라서 똑같은 행이나 열이 존재해도 행렬식의 값은 0이 된다. \(\begin{vmatrix}\ a & b & c \\\ \ 2a & 2b & 2c \\\ \ d & e & f \end{vmatrix} = a \begin{vmatrix}\ 2b & 2c \\\ \ e & f \end{vmatrix} - 2a \begin{vmatrix}\ b & c \\\ \ e & f \end{vmatrix} + d \begin{vmatrix}\ b & c \\\ \ 2b & 2c \end{vmatrix} = a(2bf-2ec)-2a(bf-ec)+d(2bc-2bc) = 0, \\\ \ \begin{vmatrix}\ g & 2j & j \\\ \ h & 2k & k \\\ \ i & 2l & l \end{vmatrix} = g \begin{vmatrix}\ 2k & k \\\ \ 2l & l \end{vmatrix} - h \begin{vmatrix}\ 2j & j \\\ \ 2l & l \end{vmatrix} + i \begin{vmatrix}\ 2j & j \\\ \ 2k & k \end{vmatrix} = g(2kl-2kl)-h(2jl-2jl)+i(2jk-2jk) = 0\)

8.4.3 크라메르의 법칙

2개의 미지수를 가진 연립방정식

먼저 다음과 같이 2개의 미지수를 가진 연립방정식의 해를 구하는 방법에 대해 알아보자.

• 식(8.35)

\[\begin{cases} a_{11} x_1 + a_{12} x_2 = r_1\\\ \ a_{21} x_1 + a_{22} x_2 = r_2 \end{cases}\]

위 식에 적당한 계수를 곱해,

\[\begin{cases} a_{22}(a_{11} x_1 + a_{12} x_2) = a_{22} r_1\\\ \ -a_{12}(a_{21} x_1 + a_{22} x_2) = -a_{12} r_2 \end{cases}\]

두 방정식을 더해서 $x_2$ 를 소거하면,

\[(a_{11} a_{22} - a_{12} a_{21})x_1 = a_{22} r_1 - a_{12} r_2\]

와 같은 식을 얻을 수 있다. 같은 방법으로 $x_1$ 을 소거하면,

\[(a_{11} a_{22} - a_{12} a_{21})x_2 = a_{11} r_1 - a_{12} r_2\]

과 같은 식을 얻을 수 있다. $D=a_{11} a_{22} - a_{12} a_{21}$ 로 가정한 다음, 앞서 얻은 두 식을 D로 나눠보자. 이 때 D는 0이 아니어야 한다. 그러면,

• 식(8.36)

\[\begin{cases} x_1 = \cfrac{r_1 a_{22} - a_{12} r_2}{D} =\ \cfrac{\begin{vmatrix}\ r1 & a_{12}\\\ \ r2 & a_{22} \end{vmatrix}}{D}\\\ \ x_2 = \cfrac{a_{11} r_2 - r_1 a_{21}}{D} =\ \cfrac{\begin{vmatrix}\ a_{11} & r_1\\\ \ a_{21} & r_2 \end{vmatrix}}{D} \end{cases}\]

와 같이 식(8.35)의 해를 구할 수 있다.

3개의 미지수를 가진 연립 방정식

다음과 같이 3개의 미지수를 가진 선형 연립방정식의 해를 구하는 방법에 대해 알아보자.

• 식(8.37)

\[\begin{cases} a_{11} x_1 + a_{12} x_2 + a_{13} x_3 = r_1\\\ \ a_{21} x_1 + a_{22} x_2 + a_{23} x_3 = r_2\\\ \ a_{31} x_1 + a_{32} x_2 + a_{33} x_3 = r_3 \end{cases}\]

2개의 미지수를 가진 선형 연립방정식에서 해를 구할 때 사용한 방법으로 식(8.37)의 해를 구해보자.

• 식(8.38)

\[x_1 = \cfrac{\begin{vmatrix}\ r_1 & a_{12} & a_{13}\\\ \ r_2 & a_{22} & a_{23}\\\ \ r_3 & a_{32} & a_{33} \end{vmatrix}}{D}, x_2 = \cfrac{\begin{vmatrix}\ a_{11} & r_1 & a_{13}\\\ \ a_{21} & r_2 & a_{23}\\\ \ a_{31} & r_3 & a_{33} \end{vmatrix}}{D}, x_3 = \cfrac{\begin{vmatrix}\ a_{11} & a_{12} & r_1\\\ \ a_{21} & a_{22} & r_2\\\ \ a_{31} & a_{32} & r_3 \end{vmatrix}}{D}\]

여기서 $D$는 식(8.37)의 계수를 원소로 하는 계수행렬로부터 얻은 행렬식이다. 즉, 다음과 같다.

\[D = \begin{vmatrix}\ a_{11} & a_{12} & a_{13}\\\ \ a_{21} & a_{22} & a_{23}\\\ \ a_{31} & a_{32} & a_{33} \end{vmatrix}\]

그리고 식(8.38)에서 각각의 해의 분자를 다음과 같이 두면,

• 식(8.39)

\[D_1 = \begin{vmatrix}\ \color{blue}{r_1} & a_{12} & a_{13}\\\ \ \color{blue}{r_2} & a_{22} & a_{23}\\\ \ \color{blue}{r_3} & a_{32} & a_{33} \end{vmatrix}, D_2 = \begin{vmatrix}\ a_{11} & \color{blue}{r_1} & a_{13}\\\ \ a_{21} & \color{blue}{r_2} & a_{23}\\\ \ a_{31} & \color{blue}{r_3} & a_{33} \end{vmatrix}, D_3 = \begin{vmatrix}\ a_{11} & a_{12} & \color{blue}{r_1}\\\ \ a_{21} & a_{22} & \color{blue}{r_2}\\\ \ a_{31} & a_{32} & \color{blue}{r_3} \end{vmatrix}\]

선형 연립방정식의 해인 식(8.38)은 다음과 같이 쓸 수 있다.

• 식(8.40)

\[x_1 = \cfrac{D_1}{D}, x_2 = \cfrac{D_2}{D}, x_3 = \cfrac{D_3}{D}\]

여기서 한가지 유의할 점은 식(8.39)와 같이 근의 분모 역할을 하는 행렬식 안에어 원소를 배열하는 방법이다. 식(8.39)를 잘 살펴보면 알 수 있듯이, $D$의 첨자와 같은 수를 가진 계수 열을 연립방정식 $Ax=r$ 의 $r$ 에 해당되는 열로 치환하면 된다. 즉, $x_1$ 의 경우, 분자가 $D_1$ 이므로 계수행렬에서 1열 원소인 $a_{11}, a_{21}, a_{31}$ 을 $r$의 원소인 $r_1, R_2, r_3$ 로 바꾸면 된다. 이와 같은 원칙은 미지수의 개수에 상관없이 똑같이 적용된다.

n개의 미지수를 가진 연립방정식

지금까지 해를 유도한 방법을 일반화해보자. 미지수의 수를 n개라고 가정한 선형 연립방정식의 형태는 다음과 같다.

• 식(8.41)

\[\begin{cases} a_{11} x_1 + a_{12} x_2 + \cdots + a_{1n} x_n = r_1\\\ \ a_{21} x_1 + a_{22} x_2 + \cdots + a_{2n} x_n = r_2\\\ \ \vdots\\\ \ a_{n1} x_1 + a_{n2} x_2 + \cdots + a_{nn} x_n = r_n \end{cases}\]

이 때 식(8.41)의 계수행렬의 행렬식은 다음과 같다.

\[D = \begin{vmatrix}\ a_{11} & a_{12} & \cdots & a_{1n}\\\ \ a_{21} & a_{22} & \cdots & a_{2n}\\\ \ \vdots & \vdots & \ddots & \vdots \\\ \ a_{n1} & a_{n2} & \cdots & a_{nn} \end{vmatrix}\]

$D \neq 0$ 이라는 가정 하에, 식(8.41)의 해는 다음과 같이 나타낼 수 있다.

• 식(8.42)

\[x_1 = \cfrac{D_1}{D}, x_2 = \cfrac{D_2}{D}, \cdots, x_n = \cfrac{D_n}{D}\]

여기서 근의 분자에 해당되는 $D_1, D_2, \cdots, D_n$ 은 다음과 같다.

\[D_1 = \begin{vmatrix}\ \color{blue}{r_1} & a_{12} & \cdots & a_{1n}\\\ \ \color{blue}{r_2} & a_{22} & \cdots & a_{2n}\\\ \ \color{blue}{\vdots} & \vdots & \ddots & \vdots \\\ \ \color{blue}{r_n} & a_{n2} & \cdots & a_{nn} \end{vmatrix}, D_2 = \begin{vmatrix}\ a_{11} & \color{blue}{r_1} & \cdots & a_{1n}\\\ \ a_{21} & \color{blue}{r_2} & \cdots & a_{2n}\\\ \ \vdots & \color{blue}{\vdots} & \ddots & \vdots \\\ \ a_{n1} & \color{blue}{r_n} & \cdots & a_{nn} \end{vmatrix}, \cdots, D_n = \begin{vmatrix}\ a_{11} & a_{12} & \cdots & \color{blue}{r_1}\\\ \ a_{21} & a_{22} & \cdots & \color{blue}{r_2}\\\ \ \vdots & \vdots & \ddots & \color{blue}{\vdots} \\\ \ a_{n1} & a_{n2} & \cdots & \color{blue}{r_n} \end{vmatrix}\]

식(8.42)는 크라메르 법칙^{Cramer’s rule} 에 따라 구한 선형 연립방정식의 일반적인 해의 형태를 나타낸 것이다.

8.5 역행렬

행렬 A에 대한 역행렬^{inverse matrix} 은 $A^{-1}$ 로 표시하는데, 행렬과 그 역행렬과의 관계는 다음과 같이 정의한다.

• 식(8.43)

\[AA^{-1} = A^{-1}A = I\]

모든 행렬에 대한 역행렬이 존재하는 것은 아니다. 역행렬을 갖는 행렬을 정칙행렬^{nonsingular matrix} , 역행렬을 갖지 못하는 행렬을 특이행렬^{singular matrix} 이라고 한다. 이 절에서는 정방행렬의 역행렬에 대해서만 살펴볼 것이다.

역행렬의 유일성

행렬이 역행렬을 갖는다면, 그 역행렬은 여러 개 존재할 수 없는 유일한 것이다.

행렬 B와 C가 행렬 A의 역행렬이라고 가정하면 다음과 같이 표현할 수 있다.

\[AB = I, CA = I\]

위의 등식을 이용하면 다음과 같은 등식이 성립함을 알 수 있다.

\[B = IB = (CA)B = C(AB) = CI = C\]

결과적으로 $B=C$ 가 된다. 이는 행렬 A의 역행렬이 두 개라는 말이 아니라 동일한 것을 다른 문자로 표현한 것일 뿐이다. 그러므로 역행렬은 여러 개 존재하지 않고, 유일하게 존재한다는 사실을 알 수 있다.

역행렬의 계산

이제 역행렬을 계산하는 방법에 대해 알아보자. 먼저 다음과 같은 2×2 행렬이 있다고 가정해보자.

\[A = \begin{bmatrix}\ a_{11} & a_{12}\\\ \ a_{21} & a_{22} \end{bmatrix}\]

행렬 A의 역행렬은 다음과 같이 계산한다.

\[A^{-1} = \cfrac{1}{\det A} \begin{bmatrix}\ a_{22} & -a_{12}\\\ \ -a_{21} & a_{11} \end{bmatrix}\]

역행렬 계산을 n×n 행렬로 일반화하면 다음과 같이 나타낼 수 있다. 여기서 $C_{11}, \cdots, C_{nn}$ 으로 표현된 것은 8.4절에서 논의했던 여인자다.

• 식(8.45)

\[A^{-1} = \cfrac{1}{\det A} \begin{bmatrix}\ C_{11} & C_{21} & \cdots & C_{n1}\\\ \ C_{12} & C_{22} & \cdots & C_{n2}\\\ \ \vdots & \vdots & \ddots & \vdots \\\ \ C_{1n} & C_{2n} & \cdots & C_{nn} \end{bmatrix}\]

식(8.43)을 이용하여 3×3 행렬의 역행렬을 구해보자. 먼저 3×3 행렬 A를 다음과 같이 두자.

\[A = \begin{bmatrix}\ a_{11} & a_{12} & a_{13}\\\ \ a_{21} & a_{22} & a_{23}\\\ \ a_{31} & a_{32} & a_{33} \end{bmatrix}\]

행렬 A의 역행렬은 다음과 같이 계산한다.

\[A^{-1} = \cfrac{1}{\det A} \begin{bmatrix}\ C_{11} & C_{21} & C_{31}\\\ \ C_{12} & C_{22} & C_{32}\\\ \ C_{13} & C_{23} & C_{33} \end{bmatrix}\]

식(8.43)을 잘 기억해 두면 모든 정방행렬의 역행렬을 계산할 수 있다. 특히 $n=2$ 인 경우인 2×2 행렬의 역행렬은 자주 쓰이므로 식(8.44)를 잘 기억해 두기 바란다.

역행렬의 성질

역행렬의 성질은 다음과 같이 정리할 수 있다.

• $(A^{-1})^{-1} = A$
• $(A^{-1})^T = (A^T)^{-1}$
• $(AB)^{-1} = B^{-1}A^{-1}$
• 역행렬이 존재하기 위한 필요충분조건은 $\det A \neq 0$

위와 같은 역행렬의 성질을 잘 활용하면 행렬에 관한 계산을 좀 더 간편하게 할 수 있을 것이다.

Chapter 09 벡터 미분법(Vector Differential Calculus)

알아 두어야 할 개념과 공식

1. 벡터의 비교

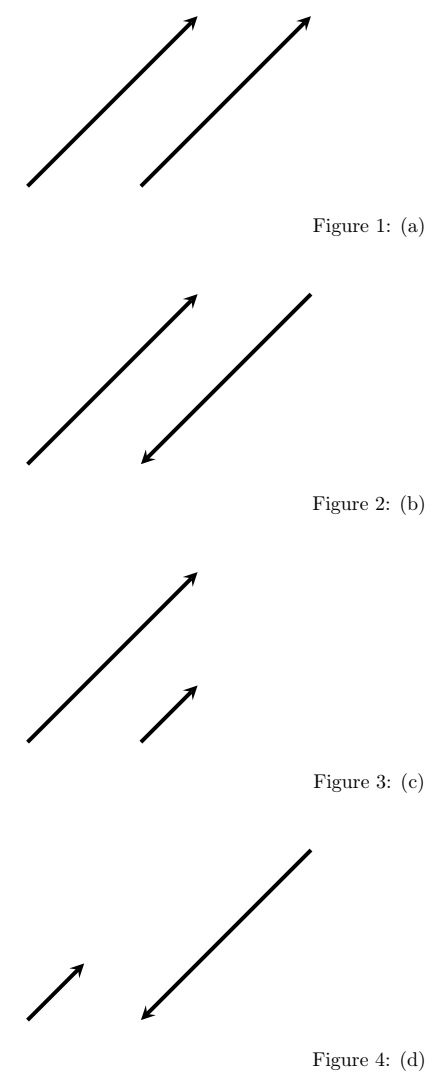
벡터 a와 b가 존재할 때, 두 벤턱의 방향과 크기가 같다면 두 벡터는 ‘같다’고 하며, a=b로 표현한다. 따라서 위치가 다르더라도 방향과 크기만 같으면 두 벡터는 같다고 할 수 있다. 아래 그림에서 (a)의 경우가 이에 해당한다. (b)는 크기는 같지만 방향이 다른 벡터, (c)는 방향은 같지만 크기가 다른 벡터, (d)는 크기도 방향도 다른 벡터를 나타낸 것이다.

2. 영벡터와 단위벡터

원점 (0,0,0)은 방향이 없고, 크기도 0이기 때문에 영벡터^{zero vector} 라고 하고, 0으로 나타낸다. 그리고 크기가 1인 벡터를 단위벡터^{unit vector} 라고 한다. 직교 좌표계에서 $x,y,z$ 의 방향으로 각각 크기가 1인 벡터를 $i,j,k$ 로 나타내는데, 이들이 바로 각각의 축 상에서의 단위 벡터다.

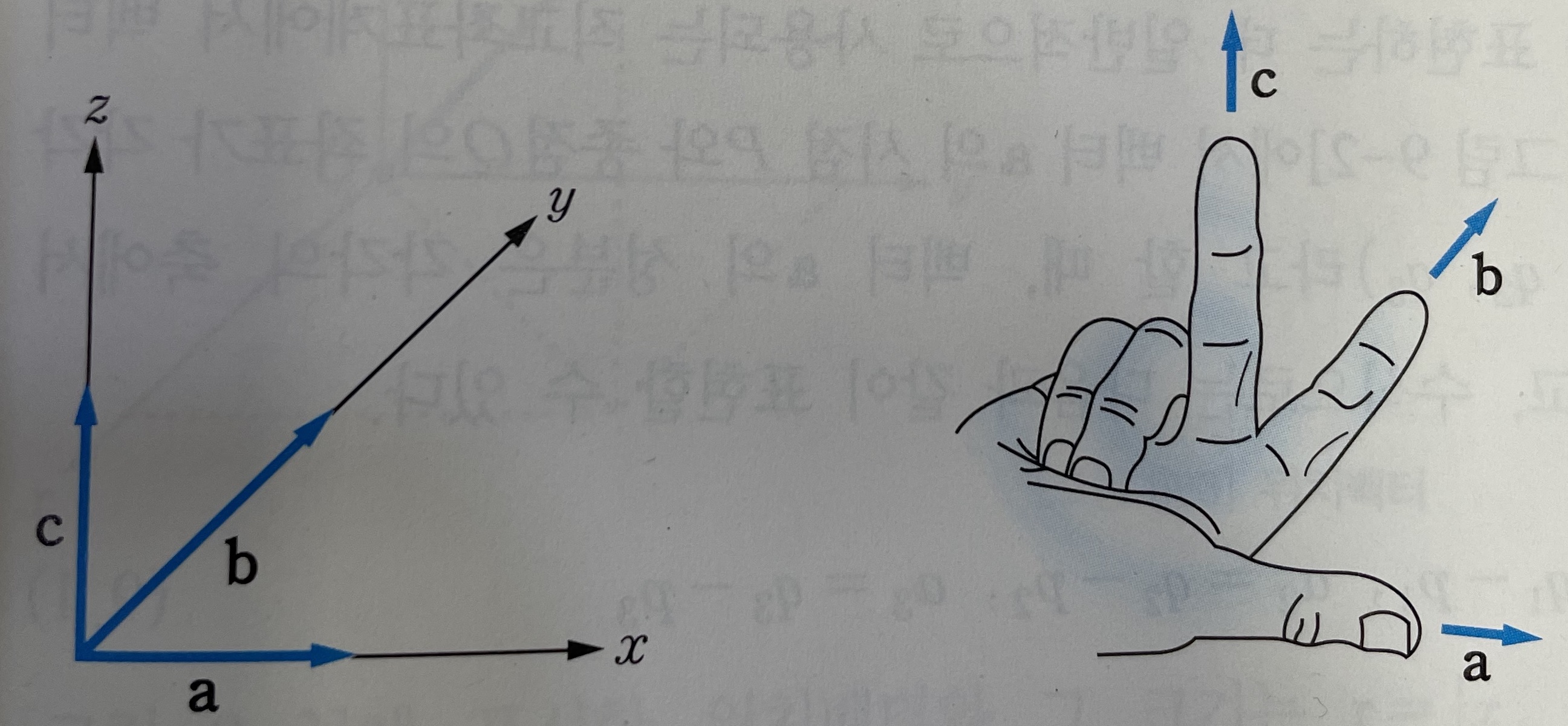
3. 오른손 법칙과 오른손 좌표계

좌표축 위의 세 벡터 $a, b, c$ 의 방향을 그림과 같이 오른손을 폈을 때 엄지, 검지, 중지가 가리키는 방향이라 가정하자. 벡터 a를 벡터 b의 방향 $\theta$ 만큼 회전 시킬 때의 벡터 c의 방향은, 오른나사^{right-handed screw}를 돌릴 때의 회전 방향에 따른 진행 방향과 일치한다. 이와 같이 오른손 법칙이 적용되는 좌표계를 오른손 좌표계라고 한다.

9.1 벡터의 기본 개념

스칼라^scalar 는 크기에 의해서만 결정되는 양이고, 벡터^vector 는 크기와 방향에 의해 결정되는 양이다. 예를 들어, 질량과 속력은 스칼라이고, 힘과 속도는 크기와 방향을 가지므로 벡터에 해당된다.

벡터의 표현

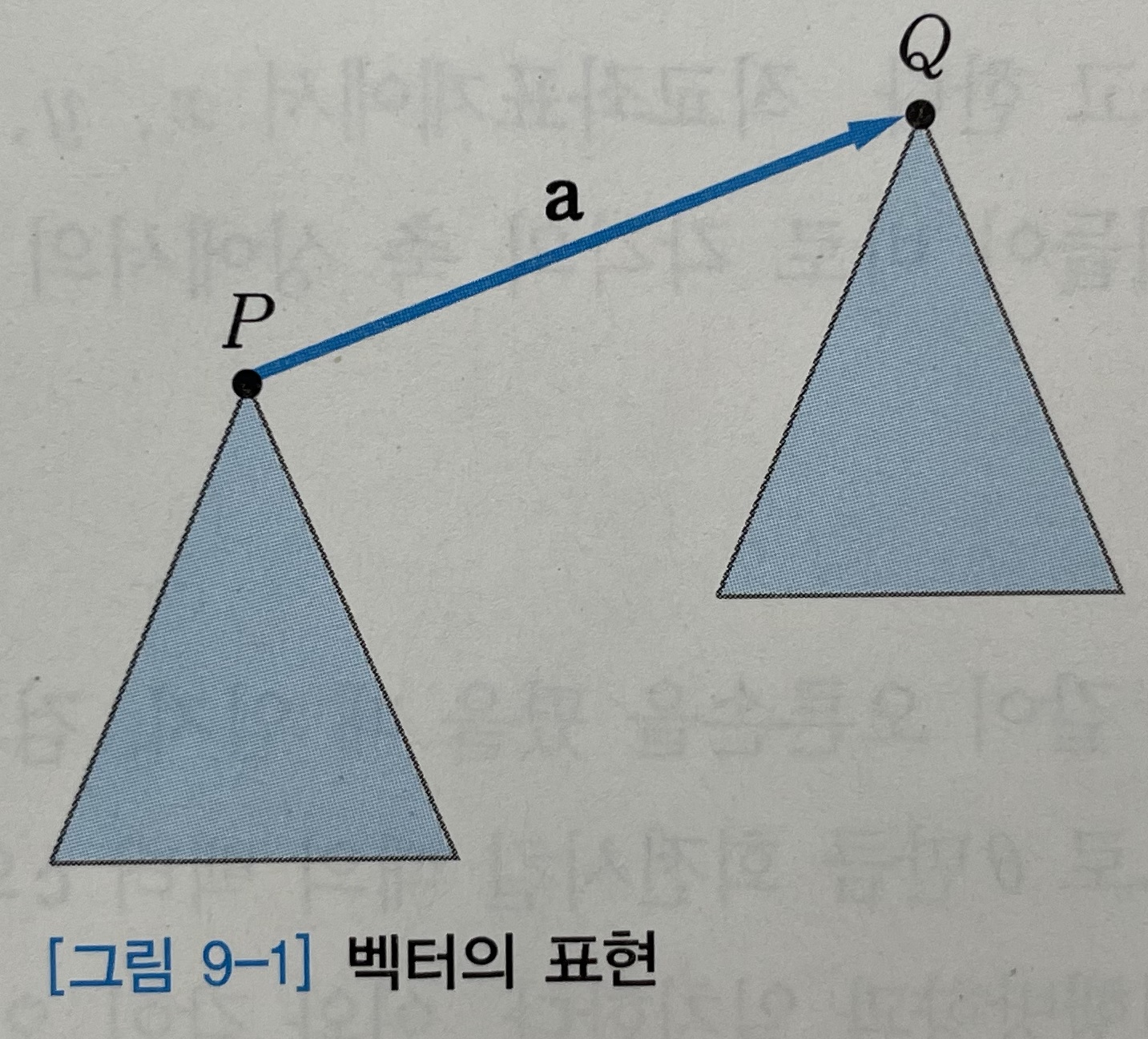
벡터는 화살표로 나타내는데, 벡터가 시작되는 화살표의 꼬리를 시점^{initial point} 이라고 하고, 벡터의 마지막 부분인 화살표의 머리를 종점^{terminal point} 이라고 한다. [그림 9-1]에서와 같이 어떤 도형이 평행이동한 경우, 벡터 a는 시점인 P에서 종점인 Q까지의 벡터이므로 벡터 $\overrightarrow{PQ}$ 로 나타내기도 한다. 이때 방향과는 상관없이 화살표의 길이만을 나타내는 양을 벡터 a의 크기^magnitude 라 하고 $|a|$ 와 같이 나타낸다.

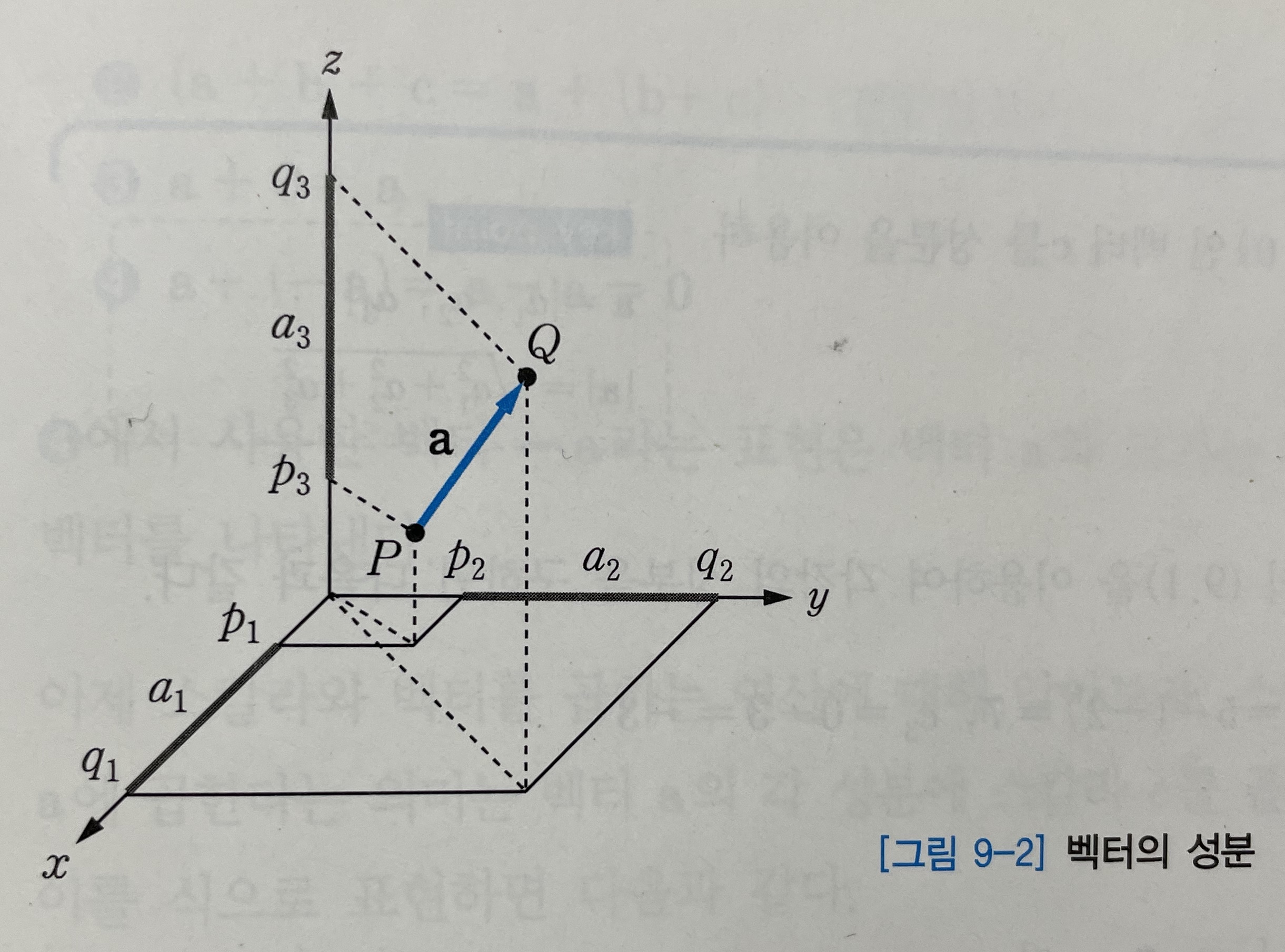
벡터의 성분

[그림 9-2]는 공간을 표현하는데 일반적으로 사용되는 직교좌표계에서 벡터 a를 표현한 것이다. [그림 9-2]에서 벡터 a의 시점 P와 종점 Q의 좌표가 각각 $(p_1, p_2, p_3)$ 와 $(q_1, q_2, q_3)$ 라고 할 때, 벡터 a의 성분은 각각의 축에서 $a_1, a_2, a_3$ 로 나타나고, 수식으로는 다음과 같이 표현할 수 있다.

• 식(9.1)

\[a_1 = q_1-p_1, a_2 = q_2-p_2, a_3 = q_3-p_3\]

벡터 a는 다음과 같이 성분으로 표기할 수도 있다.

• 식(9.2)

\[a = [a_1, a_2, a_3]\]

앞에서 설명한 벡터 a의 크기를 성분으로 표시하면 다음과 같다.

• 식(9.3)

\[|a| = \sqrt{a_1^2 + a_2^2 + a_3^2}\]

시점이 좌표계의 원점 (0, 0, 0)인 벡터를 위치벡터position vector 라 한다. 그러므로 종점이 $A(a_1, a_2, a_3)$ 인 위치벡터 r을 도시하면 그림 9-3과 같으며, 이 벡터의 크기는 $

r

= \sqrt{a_1^2 + a_2^2 + a_3^2}$ 이다.

• [그림 9-3]

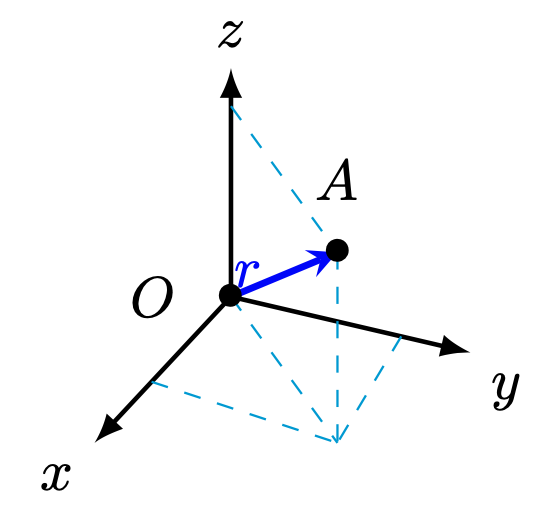
[그림 9-3]에 표시한 위치벡터와 그 크기는 $r = [x, y, z]$ 그리고 $

r

= \sqrt{x^2 + y^2 + z^2}$ 과 같이 위치벡터의 성분으로 나타낼 수 있다.

벡터의 기본 연산

벡터의 기본적이 ㄴ연산법에 대해 살펴보자. 벡터 $a = [a_1, a_2, a_3]$ 와 $b = [b_1, b_2, b_3]$ 가 있을 때, 두 벡터의 합은 다음과 같이 각각의 성분의 합으로 정의한다.

• 식(9.4)

\[a+b = [a_1+b_1, a_2+b_2, a_3+b_3]\]

[그림 9-4]는 식(9.4)를 x, y평면에서 도시한 것이다.

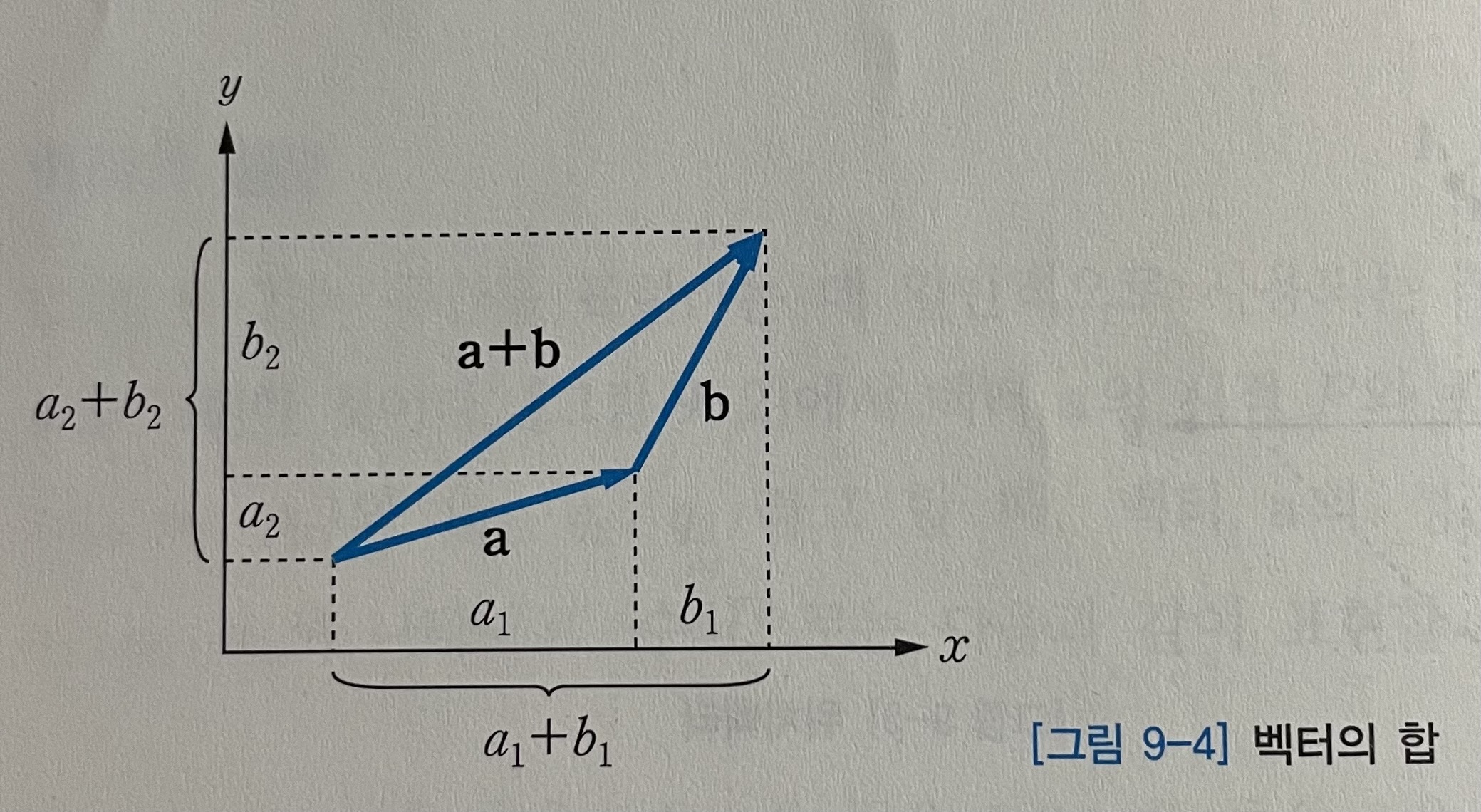
이 때 벡터의 합은 다음과 같은 성질을 갖는다.

• (1) 교환법칙: $a+b = b+a$
• (2) 결합법칙: $(a+b)+c = a+(b+c)$
• (3) $a+0=a$
• (4) $a+(-a) = a-a = 0$

(4)에서 사용한 벡터 $-a$ 라는 표현은 벡터 $a$ 와 크기는 같지만 방향이 반대인 벡터를 나타낸다.

이제 스칼라와 벡터를 곱하는 여산에 대해 알아보자. 스칼라량 c(실수)를 벡터 $a$ 에 곱한다는 의미는 벡터 $a$ 의 각 성분에 스칼라 c를 곱한다는 뜻이다. 따라서 이를 식으로 표현하면 다음과 같다.

• 식(9.5)

\[ca = [c \textbf{a_1}, c \textbf{a_2}, c \textbf{a_3}]\]

스칼라량을 벡터에 곱하는 연산은 다음과 같은 성질을 갖는다.

• (1) $c(a+b) = ca+cb$
• (2) $(c+d)a = ca + da$
• (3) $c(da) = (cd)a = cda$

각각의 축에서 크기가 1인 단위벡터^{unit vector} i, j, k의 합을 이용하여 임의의 벡터를 표현할 수도 있다. 먼저 각각 x, y, z 축의 단위벡터인 i, j, k를 성분으로 나타내면

• 식(9.6)

\[i = [1, 0, 0], j = [0, 1, 0], k = [0, 0, 1]\]

이고, [그림 9-5]는 단위벡터 i, j, k를 도시한 것이다.

성분 $a_1, a_2, a_3$ 를 갖는 벡터 $a$ 는 식(9.6)을 이용하면 다음과 같이 나타낼 수 있다.

• 식(9.7)

\[a = [a_1, a_2, a_3] = a_1 i + a_2 j + a_3 k\]

9.2 벡터의 내적

벡터의 내적^{inner product} 은 벡터의 곱이 스칼라량으로 산출되는 연산이다. 두 벡터 a와 b의 내적을 정의하면 다음과 같다.

• 식(9.8)

\[a \cdot b = |a||b|\cos \theta\]

식(9.8)에서 $\theta$ 는 두 벡터의 사잇각을 의미한다. 두 벡터가 모두 0이 나닌 경우의 사잇각이다. 왜냐하면 영벡터와의 사잇각은 정의되지 않기 때문이다.

두 벡터가 각각 $a=[a_1, a_2, a_3], b=[b_1, b_2, b_3]$ 이면 다음과 같이 벡터의 성분을 이용하여 내적을 표현할 수도 있다.

• 식(9.9) \(a \cdot b = a_1 b_1 + a_2 b_2 + a_3 b_3\)

[그림 9-6]은 두 벡터의 내적과 사잇각과의 관계를 나타낸 것이다.

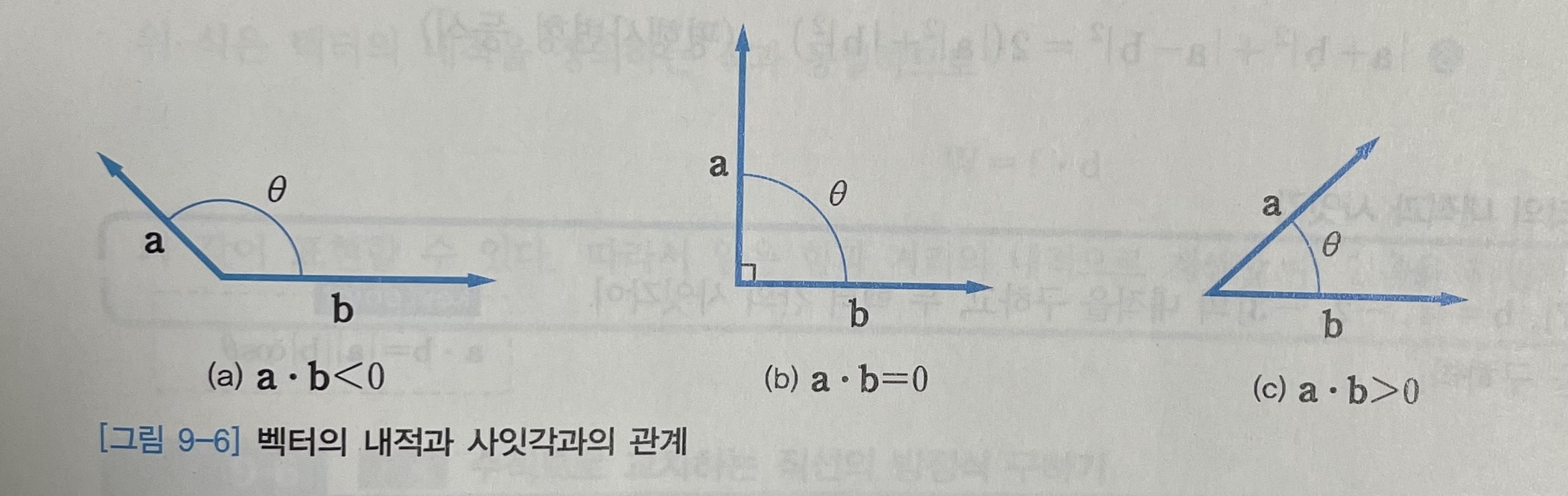
[그림 9-6]의 (b)와 같은 경우, 즉

• 식(9.10)

\[a \cdot b = 0\]

이 성립할 때 두 벡터 a와 b는 직교^orthogonal 한다고 한다. 이와 같이 두 벡터가 직교하는 성질 (두 벡터의 내적이 0일 때)을 직교성^{orthogonality} 이라고 한다.

식(9.8)에서의 두 벡터를 동일한 벡터 a라고 가정하면 벡터의 내적, 즉 자신과의 내적은 다음과 같이 정의한다.

• 식(9.11)

\[a \cdot a = |a|^2\]

따라서 다음과 같이 쓸 수 있다.

• 식(9.12)

\[|a| = \sqrt {a \cdot a}\]

또한 두 벡터의 사잇각에 대한 코사인 값은 다음과 같이 나타낼 수 있다.

• 식(9.13)

\[\cos \theta = \cfrac{a \cdot b}{|a||b|} = \cfrac{a \cdot b}{\sqrt{a \cdot a} \sqrt{b \cdot b}}\]

벡터의 내적에 관한 성질

벡터 a, b, c로 내적에 대한 성질을 정리하면 다음과 같다. 이 때 m과 n은 스칼라량으로, 실수다.

• (1) 대칭성: $a \cdot b = b \cdot a$
• (2) 선형성: $(m \textbf{a}+n \textbf{b}) \cdot \textbf{c} = m \textbf{a \cdot b} + n \textbf{b \cdot c}$

• (3) 양의 정치성: $a \cdot a =

  a

  ^2 = 0$ 이면 $a = 0$

• (4) 슈발츠 부등식: $

  a \cdot b

  \leq

  a

  b

  $

• (5) 삼각형 부등식: $

  a+b

  \leq

  a

  +

  b

  $

• (6) 평행사변형 등식: $

  a+b

  ^2+

  a-b

  ^2 = 2(

  a

  ^2+

  b

  ^2)$

9.3 벡터의 외적

벡터 a와 b의 외적^{cross product} 은 다음과 같이 정의된다.

• 식(9.14)

\[v=a \times b\]

벡터의 내적은 스칼라로 나타나는 데 비해, 벡터의 외적은 벡터로 나타난다는 사실을 알 수 있다.

식(9.14)에 표현한 벡터의 외적의 크기는 다음과 같다.

• 식(9.15)

\[|v| = |a||b|\sin \theta\]

식(9.15)는 벡터 a와 b로 이루어지는 평행사변형의 면적을 나타낸다. [그림 9-8]은 벡터 a와 b로 이루어지는 평행사변형과 그 외적 $a \times b$ 를 나타낸 것이다.

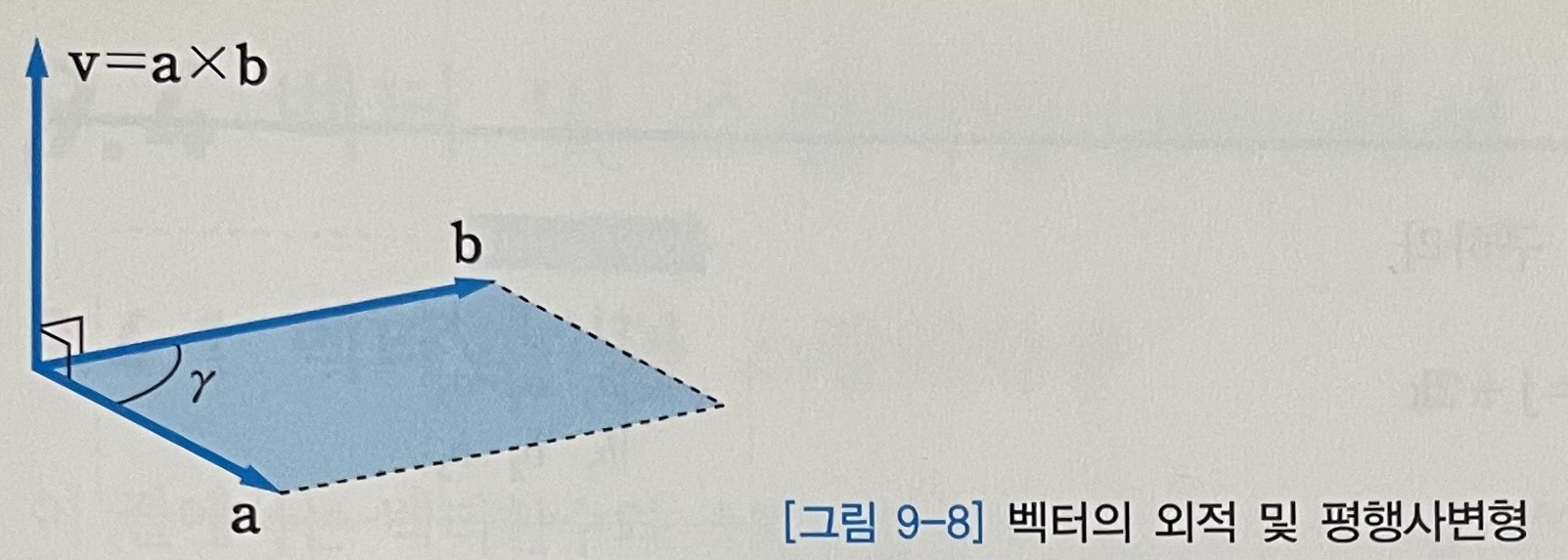
벡터의 외적 $a \times b$ 의 방향은 벡터 a와 b 모두에 수직인 방향(지면의 아랫방향)이다. 또 $a \times b$ 의 방향은 a, b, v의 순서대로 오른손 법칙을 만족한다.

벡터의 외적을 성분으로 표시하면 다음과 같다.

• 식(9.16)

\[v = [v_1, v_2, v_3] = [a_2b_3 - a_3b_2, a_3b_1 - a_1b_3, a_1b_2 - a_2b_1]\]

3차 행렬식을 이용하면 식(9.16)을 다음과 같이 나타낼 수 있다.

• 식(9.17)

\[v = v_1 \textbf{i} + v_2 \textbf{j} + v_3 \textbf{k} = \begin{vmatrix}\ \textbf{i} & \textbf{j} & \textbf{k}\\\ \ a_1 & a_2 & a_3\\\ \ b_1 & b_2 & b_3 \end{vmatrix}\]

벡터의 외적에 관한 성질

벡터 a, b, c를 사용하여 벡터의 외적에 대한 성질을 정리해보자.

• (1) $a \times (b + c) = (a \times b) + (a \times c)$
• (2) $(a+b) \times c = (a \times c) + (b \times c)$
• (3) $b \times a = -(a \times b)$
• (4) $a \times (b \times c) \neq (a \times b) \times c$

위 식에서 (1)과 (2)는 분배법칙이 성립한다는 사실을 나타내고 (3)과 (4)는 각각 교환법칙과 결합법칙이 성립하지 않는다는 사실을 나타낸 것이다.

9.4 벡터 및 스칼라 함수와 곡선

9.4.1 벡터 함수와 스칼라 함수

이 절에서는 벡터함수와 스칼라함수의 미분법을 살펴볼 것이다. 먼저 벡터함수에 대해 논의하기 위해 9.1절에서 설명한 위치벡터를 이용할 것이다. 위치벡터를 단위벡터로 나타낸면 다음과 같이 쓸 수 있다.

• 식(9.18)

\[r = [x, y, z] = x \textbf{i} + y \textbf{j} + z \textbf{k}\]

위 식에서 성분 x, y, z를 임의의 변수를 가진 함수 $r_1(P), r_2(P), r_3(P)$ 라고 생각하면, 다음과 같이 나타낼 수 있다.

• 식(9.19)

\[r = r(P) = [r_1(P), r_2(P), r_3(P)] = r_1(P)i + r_2(P)j + r_3(P)k\]

식(9.19)는 벡터를 함수값으로 하고 있따. 따라서 $r(P)$ 와 같은 형태를 벡터함수^{vector function} 라고 한다. 또 이와 같은 함수가 정의되어 있는 공간을 벡터장^{vector field} 이라고 한다.

식(9.19)에서 각각의 성분 $r_1(P), r_2(P), r_3(P)$ 는 점 P에서 함수값이 스칼라로 주어지는 함수를 의미한다. 이와 같은 함수는 직교좌표계에서

• 식(9.20)

\[f = f(P) = f(x, y, z)\]

와 같이 정의할 수 있으며, 이를 스칼라함수^{scalar function} 라고 한다. 스칼라함수가 정의되어 있는 공간은 스칼라장^{scalar field} 이라고 한다.

벡터함수를 직교좌표계에서 정의하면 다음과 같이 표현할 수도 있다.

• 식(9.21)

\[r(P) = r(x, y, z) = [r_1(x, y, z) r_2(x, y, z), r_3(x, y, z)]\]

공간상에 존재하는 임의의 곡선에서 각 점에서의 접선벡터가 벡터함수의 예다. 점의 위치에 따라 크기와 방향이 달라지기 때문이다. 반면, 고정된 점에서 임의의 점까지의 거리를 나타내는 함수는 스칼라함수다. 방향은 상관없이 크기(거리)만 달라지는 함수이기 때문이다.

벡터함수의 미분

다음과 같은 벡터함수 r(t)가 존재할 때

• 식(9.22)

\[r(t) = [r_1(t), r_2(t), r_3(t)] = r_1(t)i + r_2(t)j + r_3(t)k\]

벡터함수 r(t)의 도함수 $r’(t)$ 는 다음과 같이 정의한다.

• 식(9.23)

\[r'(t) = [r_1'(t), r_2'(t), r_3'(t)]\]

벡터함수에서의 각 성분은 스칼라함수이므로 벡터함수의 비분법은 스칼라함수의 미분법과 동일하다.

다음은 벡터함수의 미분에 관한 법칙이다.

• (1) $(u+v)’ = u’ + v’$
• (2) $(u \cdot v)’ = u’ \cdot v + u \cdot v’$
• (3) $(u \times v)’ = u’ \times v + u \ times v’$
• (4) $(u v w)’ = (u’ v w) + (u v’ w) + (u v w’)$

벡터함수의 편도함수도 스칼라함수의 미분법과 똑같이 적용된다는 사실도 기억해 두자.

9.4.2 벡터함수와 곡선

다음과 같은 벡터함수 r(t)는 3차원 공간에서 곡선 C를 나타내는 것으로 생각할 수 있다.

• 식(9.24)

\[r(t) = [x(t), y(t), z(t)] = x(t)i + y(t)j + z(t)k\]

그러므로 식(9.24)는 t를 매개변수로 하는 곡선의 방정식이 된다. 식(9.24)는 곡선의 방향을 나타내기도 하는데, t가 증가할 때 곡선이 향하는 방향을 곡선의 양의 방향^{positive sense} , t가 감소할 때 곡선이 향하는 방향을 곡선의 음의 방향^{negative sense} 이라고 한다.

대표적인 곡선의 벡터함수 표현

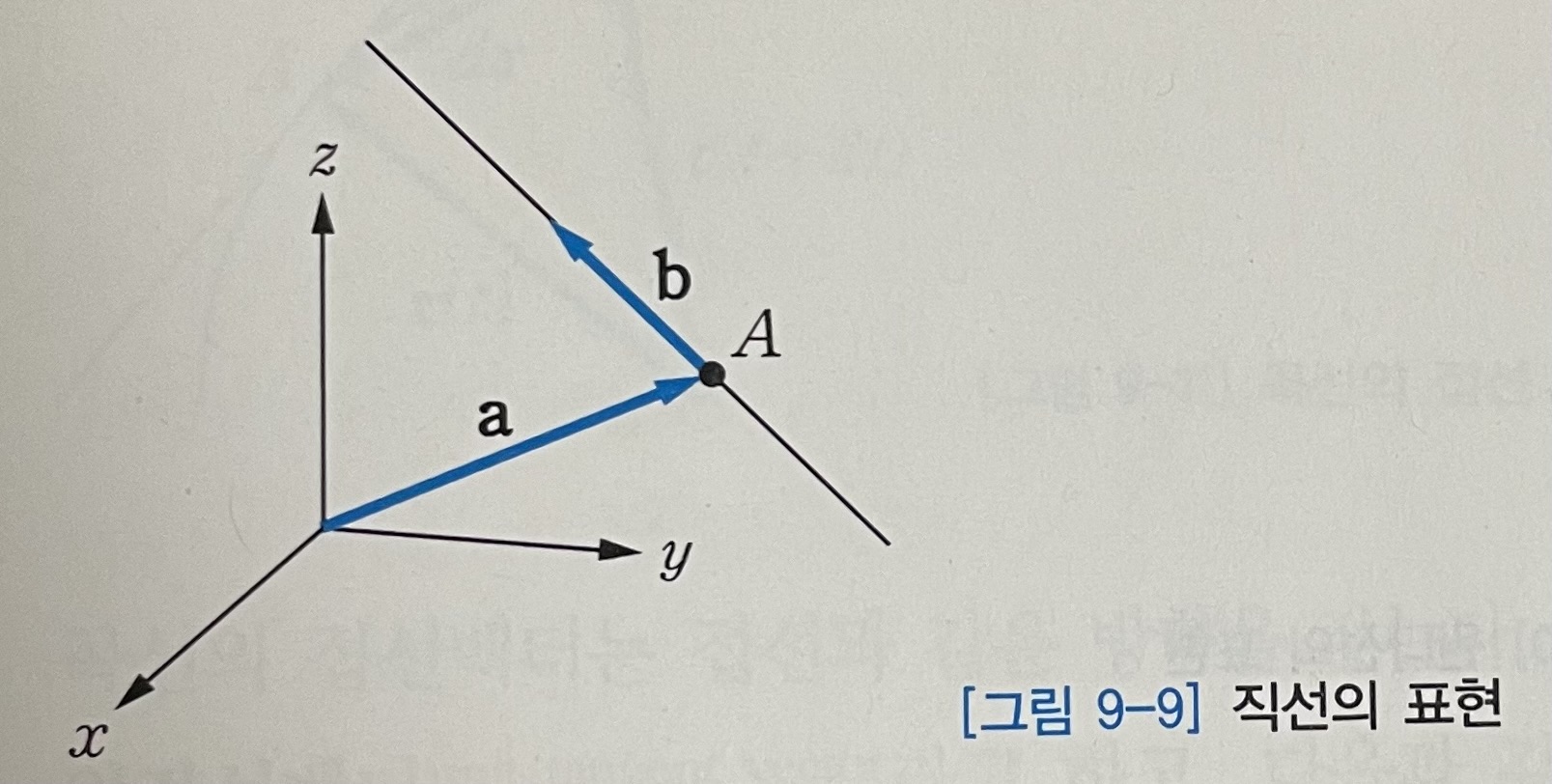
[그림 9-9]와 같이 점 A를 지나고, 상수벡터 b의 방향으로 진행하는 직선은 다음과 같이 나타낸다.

• 식(9.25)

\[r(t) = \textbf{a} + t \textbf{b} = [a_1 + tb_1, a_2 + tb_2, a_3 + tb_3]\]

식(9.25)에서 벡터 a는 점 A의 위치를 나타내는 위치벡터다.

원점을 중심으로 하고, xy평면상에 존재하는 타원은 다음과 같이 나타낸다.

• 식(9.26)

\[r(t) = a \cos t \textbf{i} + b \sin t \textbf{j} = [a \cos t, b \sin t, 0]\]

식(9.26)에서 $x(t) = a \cos t, y(t) = b \sin t$ 이므로

\[\cos t = \cfrac{x}{a}, \sin t \ \cfrac{y}{b}\]

이고, 각각 양변을 제곡하여 두 식을 더하면 다음과 같다.

\[\cfrac{x^2}{a^2}+\cfrac{y^2}{b^2} = \cos^2t + \sin^2t\]

이 때, $\cos^2t + \sin^2t = 1, z=0$ 이므로 다음과 같은 타원의 방정식이 된다.

\[\cfrac{x^2}{a^2}+\cfrac{y^2}{b^2} = 1, z = 0\]

위의 식에서 $a \eq b$ 이면

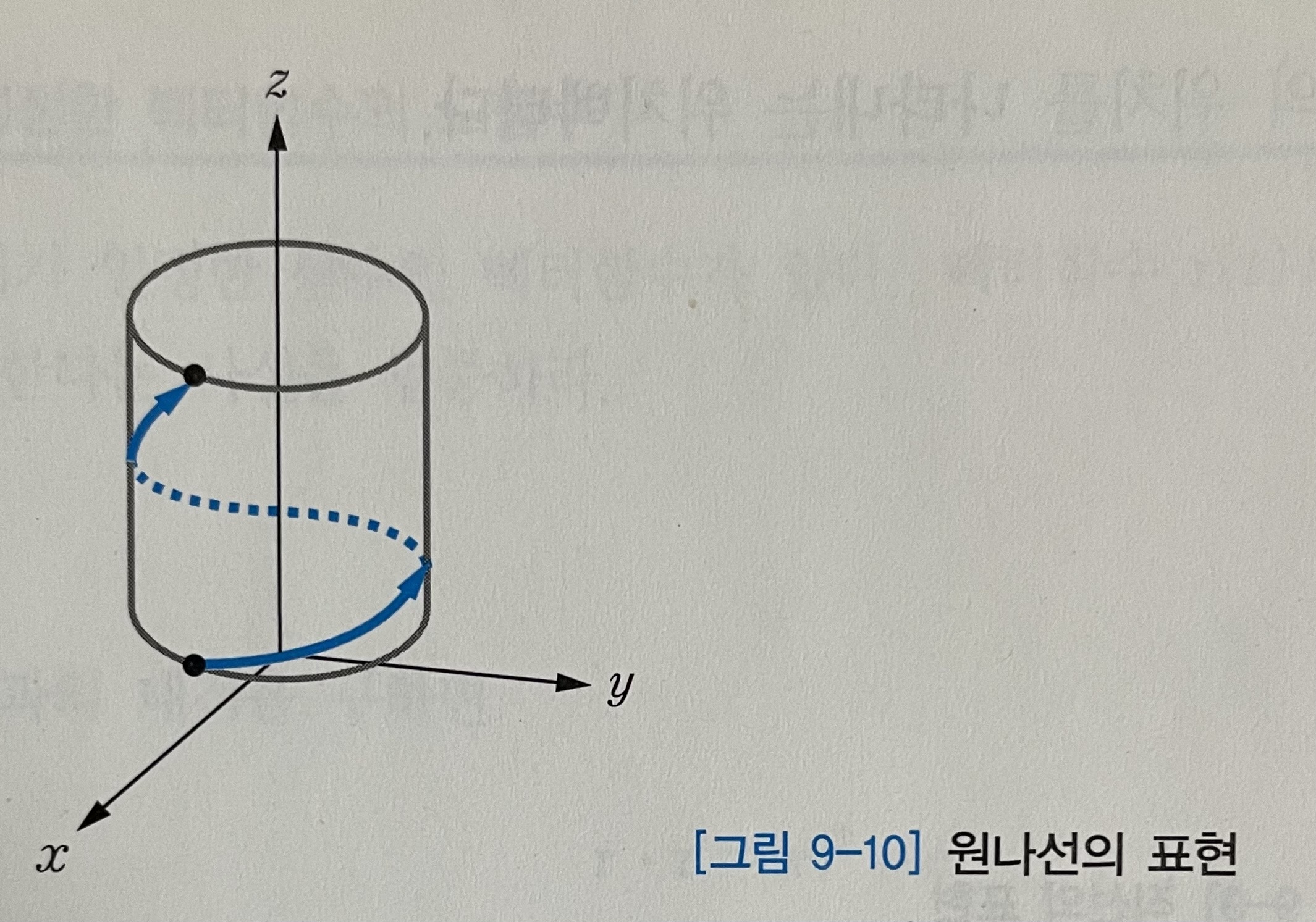
\[x^2+y^2 = a^2, z=0\]

과 같이 반지름이 a인 원의 방정식이 된다. [그림 9-10]과 같이 원기둥을 감으며 이동하는 곡선을 원나선^{circular helix} 이라고 하며, 원나선은 다음과 같은 벡터함수로도 표현할 수 있다.

• 식(9.27)

\[r(t) = a \cos t \textbf{i} + b \sin t \textbf{j} + ct \textbf{k} = [a \cos t, b \sin t, ct]\]

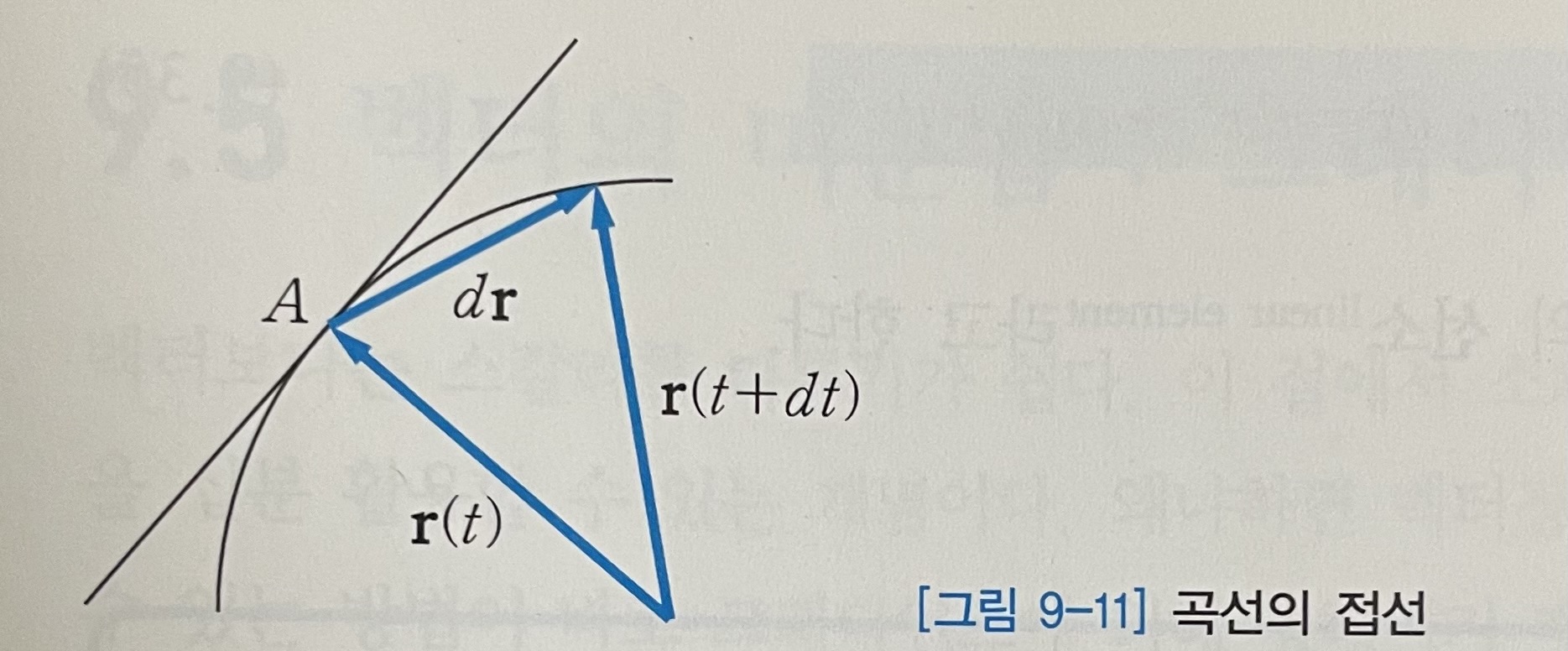
곡선의 접선, 길이, 호의 길이

곡선 위에 있는 임의의 점 A에서 곡선의 양의 방향에 따라 이동하는 경우, 미소 변위 $d \textbf{r}$ 은 다음과 같이 표현할 수 있다. ([그림 9-11]).

• 식(9.28)

\[d \textbf{r} = \textbf{r}(t +dt) - \textbf{r}(t)\]

식(9.28)에서 $dt \rightarrow 0$ 이 되면 곡선에 접하는 벡터가 된다. 그러므로 곡선의 접선벡터^{tangent vector} 는 다음과 같은 식으로 나타낼 수 있다.

• 식(9.29)

\[\textbf{r}'(t) = \cfrac{d \textbf{r}(t)}{dt} = \cfrac{d}{dt}[\textbf{r}(t+dt)-\textbf{r}(t)]\]

곡선의 접선벡터는 접선과 같은 방향을 갖는다. 또 $\textbf{r}’(t)$ 방향의 단위벡터를 단위접선벡터^{unit tangent vector} 라고 하고, 다음과 같이 표현한다.

• 식(9.30)

\[u = \cfrac{\,dr}{|dr|} = \cfrac{r'}{|r'|}\]

구간 $t_0 \leq t \leq t_n$ 인 곡선 $r(t)$ 의 길이^length 는 다음 식으로 구할 수 있다.

• 식(9.31)

\[l = \int_{t_0}^{t_n} \sqrt{r'(t) \cdot r'(t)}dt\]

식(9.31)의 적분구간에서 상한을 나타내는 상수 $t_n$ 을 변수인 t로 바꾸면, 다음과 같이 호의 길이함수^{arc length function} 를 구할 수 있다.

• 식(9.32)

\[s(t) = \int_{t_0}^{t} \sqrt{r'(t) \cdot r'(t)}d \tilde t\]

식(9.32)에서 적분변수로 $\tilde t$ 를 사용한 이유는 적분의 상한으로 t를 사용했기 대문이다. 일반적으로 $t_0=0$ 으로 하는 경우가 많다.

식(9.32)를 미분하여 제곱하면 다음과 같은 식을 얻을 수 있다.

• 식(9.33)

\[\left(\cfrac{ds}{dt}\right)^2 = \cfrac{d\textbf{r}}{dt}\cdot\cfrac{d\textbf{r}}{dt} = |\textbf{r}'(t)|^2 = \left(\cfrac{dx}{dt}\right)^2+\left(\cfrac{dy}{dt}\right)^2+\left(\cfrac{dz}{dt}\right)^2\]

곡선의 벡터함수를

\[\textbf{r}(t) = [x(t), y(t), z(t)] = x(t)\textbf{i} + y(t)\textbf{j} + z(t)\textbf{k}\]

와 같이 표현하므로 $d\textbf{r}$ 은 다음과 같이 쓸 수 있다.

• 식(9.34)

\[d\textbf{r}(t) = [dx(t), dy(t), dz(t)] = dx(t)\textbf{i} + dy(t)\textbf{j} + dz(t)\textbf{k}\]

그러므로

• 식(9.35)

\[ds^2 = d\textbf{r} \cdot d\textbf{r} = dx^2 + dy^2 + dz^2\]

이 되고, 위의 ds를 곡선의 선소^{linear element} 라고 한다.

9.5 벡터의 미분법: 그래디언트

벡터보다는 스칼라를 다루기가 쉽다. 이 절에서 소개할 그래디언트는 그런 면을 십분 활용할 수 잇는 개념이다. 왜냐하면 벡터장을 스칼라장으로부터 얻을 수 있는 방법이 바로 그래디언트에 의해 정해지기 때문이다. 공간 변화율, 법선 벡터 등 벡터의 미분법에 해당되는 그래디언트는 유용하게 이용되는 면이 많다. 그러므로 여기서 소개되는 그래디언트의 개념을 확실히 이해하는 것은 매우 중요하다.

먼저 그래디언트^gradient 의 정의부터 알아보자. 스칼라함수 $f(x,y,z)$ 의 그래디언트는 $grad f$ 또는 $\nabla f$ 라고 표기하며, 다음과 같은 벡터함수로 나타낸다.

• 식(9.36)

\[grad f = \nabla f = \frac{\partial f}{\partial x}\textbf{i} + \frac{\partial f}{\partial y}\textbf{j} + \frac{\partial f}{\partial z}\textbf{k} = \left[\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z}\right]\]

이 때 미분연산자 $\nabla$ 만을 고려하면 다음과 같이 나타낸다.

• 식(9.37)

\[\nabla = \cfrac{\partial}{\partial x}\textbf{i} + \cfrac{\partial}{\partial y}\textbf{j} + \cfrac{\partial}{\partial z}\textbf{k}\]

방향도함수

스칼라함수 $f$ 가 공간상에서 특정 방향에 따라 변화하는 비율을 알고자 하는 것이 방향도함수^{directional derivative} 다. 공간상의 한 점 P에서 Q로 벡터 m이 진행되는 방향으로 f의 방향도함수는 다음과 같이 정의된다.

• 식(9.38)

\[D_mf = \cfrac{df}{ds} = \lim_{s \to 0} \cfrac{f(Q)-f(P)}{s}\]

식(9.38)에서 s는 점 P에서 Q까지의 거리다. 벡터 m을 단위벡터라고 가정하면 직선의 방정식은 다음과 같이 나타낼 수 잇다.

• 식(9.39)

\[r(s) = x(s)i + y(s)j + z(s)k = p_0 + sm, (s \geq 0)\]

식(9.39)에서 $P_0$ 는 점 P의 위치벡터다. 함수 f는 호의 길이 s에 대한 함수 $f[x(s), y(s), z(s)]$ 이므로, 사슬법칙을 이용하면 식 (9.38)은

\[D_mf = \cfrac{df}{ds} = \cfrac{\partial f}{\partial x}\cfrac{dx}{ds} + \cfrac{\partial f}{\partial y}\cfrac{dy}{ds} + \cfrac{\partial f}{\partial z}\cfrac{dz}{ds}\]

와 같이 되고, 결국

• 식(9.40)

\[D_mf = \cfrac{df}{ds} = \cfrac{\partial f}{\partial x}x'(s) + \cfrac{\partial f}{\partial y}y'(s) + \cfrac{\partial f}{\partial z}z'(s)\]

와 같이 표현할 수 있다. 식(9.39)를 미분하면

\[\textbf{r}'(s) = x'(s)i+y'(s)j+z'(s)k = \cfrac{d}{ds} \left[\textbf{p}_ 0 + s \textbf{m}\right] = m\]

이 된다. 또한 식(9.40)은

\[D_mf = \cfrac{\partial f}{\partial x}x'(s) + \cfrac{\partial f}{\partial y}y'(s) + \cfrac{\partial f}{\partial z}z'(s) = (x'(s)i+y'(s)j+z'(s)k) \cdot \left(\cfrac{\partial f}{\partial x}\textbf{i} + \cfrac{\partial f}{\partial y}\textbf{j} + \cfrac{\partial f}{\partial z}\textbf{k} \right) = r' \cdot \nabla f\]

가 된다. 결과적으로 방향도함수 $D_mf$ 는

• 식(9.41)

\[D_mf = \cfrac{df}{ds} = m \cdot \nabla f\]

와 같이 표현할 수 있다. 또 단위 벡터가 아닌 일반 벡터 a가 진행되는 방향으로 방향도함수는 다음과 같이 나타낸다.

\[D_af = \cfrac{df}{ds} = \cfrac{1}{|a|}a \cdot \nabla f\]

곡면법선벡터

공간 위엥서의 곡선이 다음과 같이 표현된다고 가정하자.

• 식(9.43)

\[r(t) = [x(t), y(t), z(t)] = x(t)i + y(t)j + z(t)k\]

이 곡선이 존재할 수 있는 곡면은 다음과 같이 나타난다.

• 식(9.44) \(f(x(t), y(t), z(t)) = c\)

위 식에서 c는 상수다. 그리고 위에서 나타낸 곡선의 접선벡터는 식(9.29)를 이용하면 다음과 같이 나타낼 수 있다.

\[r'(t) = x'(t)i + y'(t)j + z'(t)k\]

한편, 곡면 위의 한 점에서는 많은 접선벡터를 생각할 수 있을 것이고, 그 접선벡터들은 하나의 면을 이루게 될 것이다. 그 평면을 접평면^{tangent plane} 이라고 하며, 이 접평면에 대한 법선을 곡면법선^{surface normal} , 곡면법선과 평행인 벡터를 곡면법선벡터^{surface normal vector} 라고 한다.

식(9.44)에 사슬법칙을 적용하여 t로 미분하면 다음과 같이 된다.

\[\cfrac{df}{dt} = \cfrac{\partial f}{\partial x}x'(t) + \cfrac{\partial f}{\partial y}y'(t) + \cfrac{\partial f}{\partial z}z'(t) = \left(\cfrac{\partial f}{\partial x}\textbf{i} + \cfrac{\partial f}{\partial y}\textbf{j} + \cfrac{\partial f}{\partial z}\textbf{k} \right) \cdot (x'i+y'j+z'k) = \nabla f \cdot r' = 0\]

$\nabla f \cdot r’ = 0$ 이 되는 것은 식(9.44)에서 나타낸 것처럼 f=c(상수)이기 때문이다. 결과적으로 벡터의 직교성에 의해 $\nabla f$ 는 모든 접선 벡터 r’, 즉 접평면과 수직이라는 사실을 확인할 수 있다. 따라서 곡면을 나타내는 함수 f의 그래디언트인 $\nabla f$ 는 곡면법선벡터의 역할을 한다.

따라서 단위곡면법선벡터^{unit surface normal vector} 는 다음과 같이 계산할 수 있다.

• 식(9.46)

\[n = \cfrac{\nabla f}{|\nabla f|}\]

9.6 벡터의 미분법: 발산, 회전

9.6.1 벡터장의 발산

$v_1, v_2, v_3$를 성분으로 하는 벡터함수 v(x, y, z)가 존재할 때, v에 의해 정의되는 벡터장의 발산^divergence 은 다음과 같이 정의한다.

• 식(9.47)

\[div v = \nabla \cdot v = \cfrac{\partial v_1}{\partial x} + \cfrac{\partial v_2}{\partial y} + \cfrac{\partial v_3}{\partial z}\]

v의 성분이 $v_1, v_2, v_3$ 이기 때문에 v를 다음과 같이 나타낼 수 있다.

\[v(x,y,z) = [v_1, v_2, v_3] = v_1i + v_2j +v_3k\]

그러므로 $\nabla \cdot v$ 는 ㅏ음과 같이 계산되는 것을 알 수 있다.

\[\nabla \cdot v = \left(\cfrac{\partial}{\partial x}\textbf{i} + \cfrac{\partial}{\partial y}\textbf{j} + \cfrac{\partial}{\partial z}\textbf{k} \right) \cdot (v_1i+v_2j+v_3k)\\\ \ = \cfrac{\partial}{\partial x}v_1 + \cfrac{\partial}{\partial y}v_2 + \cfrac{\partial}{\partial z}v_3 = \cfrac{\partial v_1}{\partial x} + \cfrac{\partial v_2}{\partial y} + \cfrac{\partial v_3}{\partial z}\]

이때 $\nabla f$ 는 벡터인데 반해, 발산 $\nabla \cdot v$ 는 스칼라라는 사실을 기억해 두자.

두 번 미분가능한 스칼라함수 f(x,y,z)가 있을 때, 그래디언트는

\[\nabla f = \cfrac{\partial f}{\partial x}\textbf{i} + \cfrac{\partial f}{\partial y}\textbf{j} + \cfrac{\partial f}{\partial z}\textbf{k}\]

와 같이 표현하므로, 그래디언트에 대한 발산은 식(9.47)에 의해

\[div (\nabla f) = \nabla \cdot (\nabla f) = \left(\cfrac{\partial}{\partial x}\textbf{i} + \cfrac{\partial}{\partial y}\textbf{j} + \cfrac{\partial}{\partial z}\textbf{k} \right) \cdot \left(\cfrac{\partial f}{\partial x}\textbf{i} + \cfrac{\partial f}{\partial y}\textbf{j} + \cfrac{\partial f}{\partial z}\textbf{k}\right)\]

가 된다. 그러므로

• 식(9.48)

\[div (\nabla f) = \nabla \cdot (\nabla f) = \cfrac{\partial^2 f}{\partial x^2} + \cfrac{\partial^2 f}{\partial y^2} + \cfrac{\partial^2 f}{\partial z^2}\]

라는 식이 성립하게 되고, 결과적으로 다ㅡㅇㅁ과 같은 식을 얻게 된다.

• 식(9.49)

\[div (\nabla f) = \nabla^2 f\]

식(9.49)에서 $\nabla^2$ 을 라플라스 연산자^{Laplace operator} 라고 하고, $\nabla^2 f = 0$ 을 라플라스 방정식이라고 한다.

발산의 값이 양이면 소스^source , 음이면 싱크^sink 가 주어진다고 한다. 소스는 물이 쏟아져 나오는 수도꼭지, 싱크는 물이 빠져 나가는 배수구와 유사한 역할이라고 생각하면 된다. 즉 발산의 값이 양이면 들어오는 것이 나가는 것보다 많다는 의미이고, 발산의 값이 음이면 들어오는 것보다 나가는 것이 더 많다는 의미다. 발산의 값이 0이라는 것은 유입량과 유출량이 동일하다는 의미다.

9.6.2 벡터장의 회전

다음과 같이 $v_1, v_2, v_3$ 를 성분으로 하는 벡터 함수가 있다고 하자.

\[v(x,y,z) = [v_1, v_2, v_3] = v_1i + v_2j +v_3k\]

벡터함수 v에 의해 정의되는 벡터장의 회전^curl 은 다음과 같이 정의한다.

• 식(9.50)

\[curl \textbf{v} = \nabla \times v = \begin{vmatrix}\ i & j & k\\\ \ \frac{\nabla}{\nabla x} & \frac{\nabla}{\nabla y} & \frac{\nabla}{\nabla z}\\\ \ v_1 & v_2 & v_3 \end{vmatrix}\]

식(9.50)의 행렬식을 풀어서 다음과 같이 표현할 수 있다.

• 식(9.51)

\[curl \textbf{v} = \nabla \times v = \left( \cfrac{\partial v_3}{\partial y} - \cfrac{\partial v_2}{\partial z} \right)i + \left( \cfrac{\partial v_1}{\partial z} - \cfrac{\partial v_3}{\partial x} \right)j + \left( \cfrac{\partial v_2}{\partial x} - \cfrac{\partial v_1}{\partial y} \right)k\]

그래디언트의 회전 은 다음과 같은 결과를 낳는다.

• 식(9.52)

\[curl (\nabla f) = \nabla \times (\nabla f) = 0\]

위 식은 벡터함수가 스칼라함수의 그래디언트($\nabla f$ )라면, 그 벡터의 회전은 0(영벡터)이 된다는 사실을 나타낸다.

또한 회전의 발산 에 대해 확인해 보면

• 식(9.53)

\[div (curl \textbf{v}) = \nabla \cdot (\nabla \times v) = 0\]

과 같이 되는 것을 알 수 있다. 즉 벡터함수의 회전으로부터는 발산(들어오는 양과 나가는 양의 차이)이 발생하지 않는다는 결론을 내릴 수 있다.

Chapter 10 벡터적분법 (Vector Integral Calculus)