book: introduction to mathmatical statistics

• Hogg, McKean, Craig
• 수리통계학 개론
• http://www.kocw.net/home/cview.do?cid=7c789810ade43386: 부산대 김충락 교수님 강의
• crkim.pusan.ac.kr
  • lecture: lecture notes
  • KOCW:
    • 수리통계학 mathematical statistics(1, 2),
    • 회귀분석 regression analysis(1, 2),
    • 수리통계학 math.stat(3),
    • 생존분석 survival analysis,
  • KMOOC: R을 활용한 통계학 개론

1. Probability and Distributions

1.1 Introduction

• Statistical(random) experiment: the outcome cannot be predicted with certainty prior to the performance of the experiment.
• Sample space: collection of every possible outcome from the random experiment, and denoted by $\mathscr{C}$ .
• Event: subset of sample, and denoted by A, B, C.
• Example 1.1.1. Consider tossing a coin, then $\mathscr{C}$ = {H, T}.
• Example 1.1.2. Consider tossing two die (one red, the other white), then $\mathscr{C}$ = {(1,1), ··· , (1,6), (2,1), ··· , (6,6)}.
• Example 1.1.3. Let C denote an event of sum seven when tossing two die, then $\mathscr{C}$ = {(1,6), (2,5), ··· , (6,1)}.
• Remark 1.1.1. Two types of probability
  • (i) Relative frequancy approach.
  • (ii) Personal or subjective approach.

1.2 Set Theory

• Definition 1.2.1. If each element of set $C_1$ is also an element of set $C_2$, then $C_1$ is called subset of $C_2$, and denoted by $C_1 \subset C_2$ .
• Definition 1.2.2. If a set C has no elements, C is called the null(empty) set, and denoted by C = $\phi$ .
• Definition 1.2.3. The set of all elements that belong to at least one of $C_1$ and $C_2$ is called the union of $C_1$ and $C_2$, and denoted by $C_1 \cup C_2$ and it can be generalized to any number of sets. For example, $C_1 \cup C_2 \cup \cdots \cup C_n = \cup_{k=1}^{\infty}C_k$ .

1.3 The Probability Set Funciton

1.3.1 셈규칙

1.3.2 확률의 추가적 특성

1.4 조건부 확률과 독립성

1.4.1 독립성

1.4.2 시뮬레이션

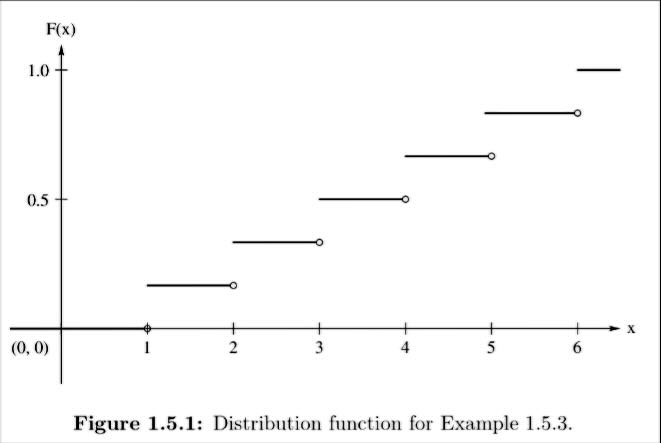
1.5 확률 변수

1.6 이산형 확률 변수

1.6.1 변환

1.7 연속형 확률 변수

1.7.1 분위수

1.7.2 변환